In ΔABC,∠B=35∘,∠C=65∘ and the bisector of ∠BAC meets BC in X. Arrange AX, BX and CX in descending order.

Video Solution
Text Solution
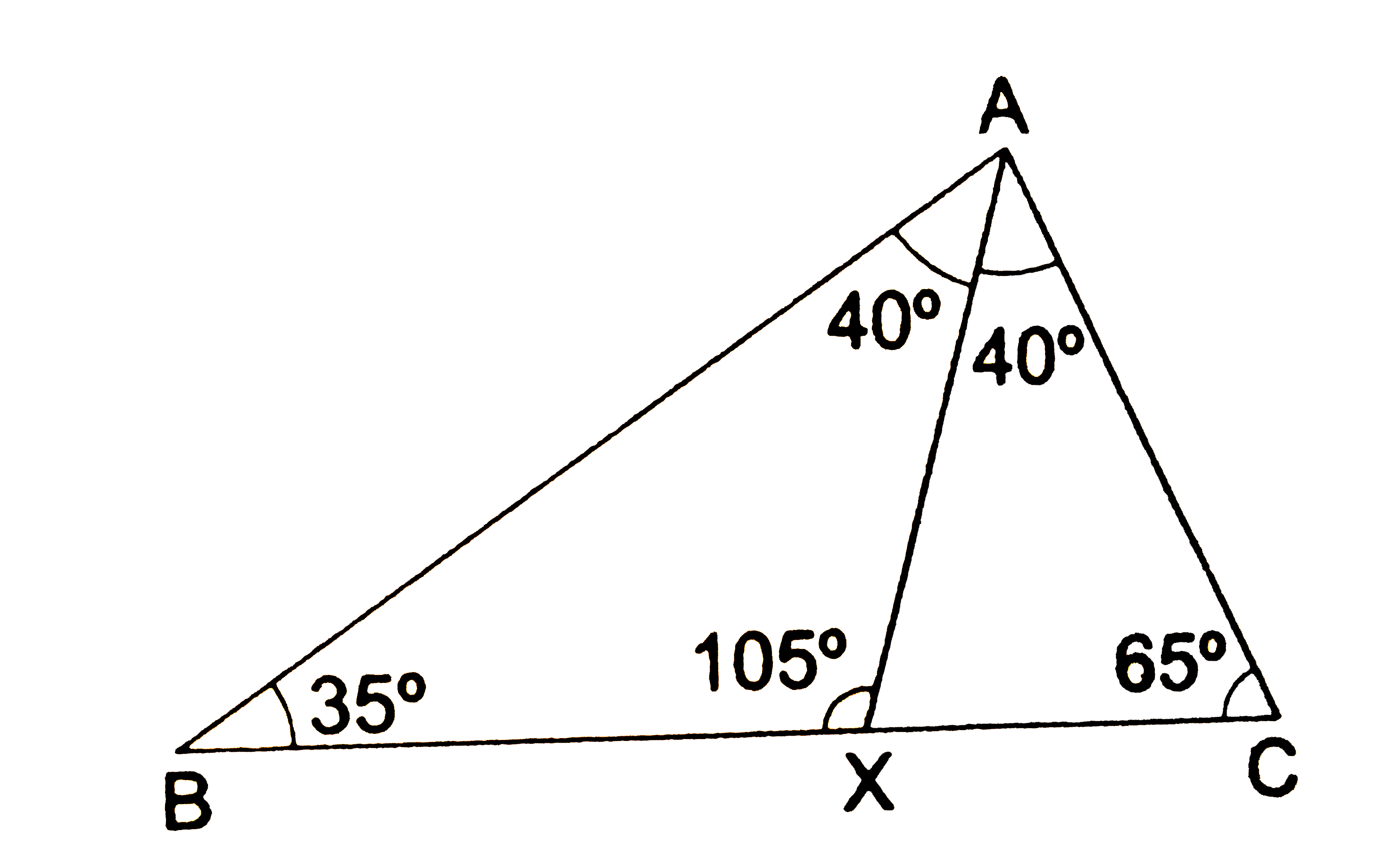
∠A+35∘+65∘=180∘⇒∠A=80∘.
∴ ∠BAX=∠CAX=40∘,∠ABX=35∘,∠ACX=65∘.
∠AXB=180∘−(40∘+35∘)=105∘.
∠BAX>∠ABX⇒BX>AX.
∠ACX>∠CAX⇒AX>CX.
∴ BX>AX>CX.
|
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionIn DeltaABC, angleB=35^(@), angleC=65^(@) and angleBAC is bisected and it meet BC at X, then put bar(AX), bar(BX) and bar(AB) in decending order-
View SolutionDeltaABC In angleB=35,angleC=65^(@) And angleBAC The bisector of X meets BC. overline(AX),overline(BX) And overline(AB) Arrange the following in descending order?
View Solution
