In ΔPQR,∠R=∠PandQR=4cmandPR=5cm . Then find the value of length of PQ×QR×PR.
To solve the problem step by step, we will use the properties of triangles, particularly focusing on the isosceles triangle formed by the given angles and sides.
1. Identify the Given Information:
- In triangle ΔPQR, we have:
- ∠R=∠P
- QR=4cm
- PR=5cm
2. Use the Isosceles Triangle Property:
- Since ∠R=∠P, triangle PQR is an isosceles triangle.
- In an isosceles triangle, the sides opposite to equal angles are equal. Therefore, PQ=PR.
3. Determine the Length of PQ:
- Since PR=5cm, we have:
- PQ=PR=5cm
4. Calculate the Product PQ×QR×PR:
- Now we can calculate the required product:
PQ×QR×PR=5cm×4cm×5cm
- First, calculate 5×4=20.
- Then, multiply 20×5=100.
5. Final Result:
- Therefore, the value of PQ×QR×PR is 100cm3.
Final Answer:
The value of PQ×QR×PR is 100cm3.
---
- In triangle ΔPQR, we have:
- ∠R=∠P
- QR=4cm
- PR=5cm
- Since ∠R=∠P, triangle PQR is an isosceles triangle.
- In an isosceles triangle, the sides opposite to equal angles are equal. Therefore, PQ=PR.
- Since PR=5cm, we have:
- PQ=PR=5cm
- Now we can calculate the required product:
PQ×QR×PR=5cm×4cm×5cm
- First, calculate 5×4=20.
- Then, multiply 20×5=100.
- Therefore, the value of PQ×QR×PR is 100cm3.
The value of PQ×QR×PR is 100cm3.
Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:OLYMPAID/ HOTS CORNER
Explore 10 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:EXERCISE (Subjective Problems) ( Long Answer Type)
Explore 5 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
If ΔABC is an obtuse angled triangle in which ∠C=110∘ then which one of the following is true ?
View SolutionIn the figure , BL⊥AC, MC⊥LN, AL=CN and BL= CM.
Prove that : △ABC≅△NML
View SolutionThe weight (in kg) of 50 students are given below
40 45 55 62 50 51 56 69 61 36
60 56 69 38 35 63 57 50 57 48
40 63 53 64 47 42 56 51 42 60
55 39 64 57 64 44 66 35 59 59
73 62 49 63 37 63 54 72 44 60
Find the mean, median and mode respectively for the given data.
View SolutionIn ΔPQR, If ∠R=∠P, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn ΔPQR,∠P=30∘,∠Q=60∘,∠R=90∘andPQ=12cm, then find PR and QR.
View SolutionIn ΔPQR,PQ=6√3cm, PR=12cm and QR=6cm , then ∠Q=
View SolutionIn an isosceles ΔPQR,PR=QR and PQ2=2PR2, then ∠R=
View SolutionΔPQR में ∠R=∠P तथा QR=4cm और PR=5cm है, तब PQ की लम्बाई है :
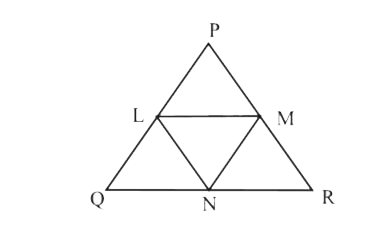
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View SolutionIn △PQR,∠R=∠P, QR=4cm and PR=5cm , Then PQ = ________
View SolutionDrawΔPQR,QR=6.0 cm,∠Q=∠R,∠P=80∘.
View SolutionIf A = ⎡⎢⎣−qrp(q+r)pr+pqpq+qr−prpq+qrqr+prqr+pr−pq⎤⎥⎦ , then |A| equals
View SolutionIn ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn ΔPQR,∠P=30∘,∠Q=60∘,∠R=90∘andPQ=12cm, then find PR and QR.
View SolutionΔPQR में, PQ = PR भुजा PR एक बिंदु x इस प्रकार है कि QR2=PR×XRसिद्ध कीजिए कि QX=QR
View SolutionDeltaPQR in PR = 8 cm, QR = 4 cm And PL = 5 cm (See the figure) Find: DeltaPQR Area of
View Solution