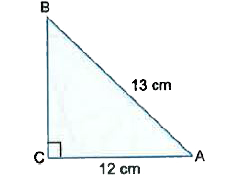
In fig. 10.11, find sin A, tan A and cot A.

Text Solution
The correct Answer is:sin A , = 133,tanA=34,cotA=43 .
|
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBook:VK GLOBAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRYExercise:PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
Explore 13 Videos
- INTRODUCTION TO TRIGONOMETRYBook:VK GLOBAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRYExercise:SELF - ASSESSMENT TEST
Explore 9 Videos
- INTRODUCTION TO TRIGONOMETRYBook:VK GLOBAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRYExercise:PROFICIENCY EXERCISE (SHORT ANSWER QUESTIONS-I)
Explore 6 Videos
- HEIGHT AND DISTANCEBook:VK GLOBAL PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:SELF ASSESSMENT TEST
Explore 11 Videos
- MID TERM TEST PAPER Book:VK GLOBAL PUBLICATIONChapter:MID TERM TEST PAPER Exercise:SECTION -D
Explore 7 Videos
Similar Questions
In Fig., find tanP and cotR . Is tanP=cotR ?
View SolutionIn Fig find ten A - cot B.
View SolutionProve that : (1 + cot A + tan A) (sin A — cos A) = sin A tan A — cot A cos A.
View SolutionProve that : (1 + cot A + tan A) (sin A — cos A) = sin A tan A — cot A cos A.
View SolutionProve that : (1 + cot A + tan A) (sin A — cos A) = sin A tan A — cot A cos A.
View Solution(1+cotA+tanA)(sinA−cosA)=sinAtanA−cotAcosA
View SolutionGiven : cosA=513
Evaluate : (i) sinA−cotA2tanA
(ii) cotA+1cosA
View SolutionProve that: sin2AtanA+cos2AcotA+2sinAcosA=tanA+cotA
View SolutionIf sinA=mn find tanA+44cotA+1
View SolutiontanA1−cotA+cotA1−tanA=1+tanA+cotA=1+secAcosecA 1+cosθ+sinθ1+cosθ−sinθ=1+sinθcosθ
View Solution
