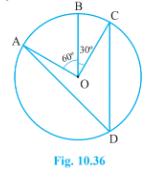
In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
∠AOC=∠AOB+∠BOC=90∘
∠AOC=2∠ADC (By Theorem 10.8)
∠ADC=12∠AOC
∠ADC=12×90=45∘
∠ADC=45∘
Similar Questions
Knowledge Check
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘
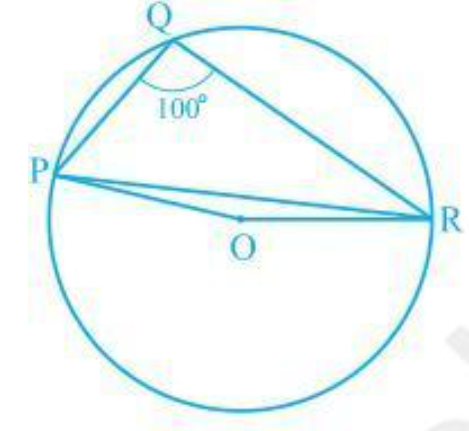
In Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
View SolutionIn Fig. PQ is tangent at a point R of the circle with centre O . If ∠TRQ=30o , find ∠PRS . (FIGURE)
View SolutionIn Fig. 10.96, if TP and TQ are tangents drawn from an external points T to a circle with centre O such that ∠TQP=60o , then ∠OPQ= (FIGURE) 25o (b) 30o (c) 40o (d) 60o
View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (FIGURE) 67o (b) 134o (c) 44o (d) 46o
View SolutionIf A,B,C are three points on a circle with centre O such that ∠AOB=90∘ and ∠BOC=120∘, then ∠ABC= 60∘ (b) 75∘ (c) 90∘ (d) 135∘
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View Solution