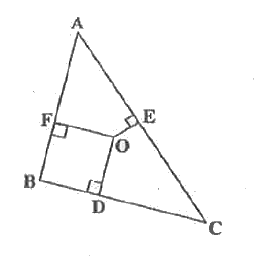
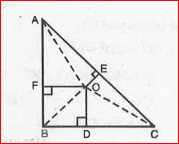
In Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for In Fig. 2.54, o is a point in the interior of a triangle ABC,ODbotBC,OEbotACandofbotAB. Show that OA^(2)+OB^(2)+OC^(2)-OD^(2)-OE^(2)-OF^(2)=AF^(2)+BD^(2)+CE^(2), by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
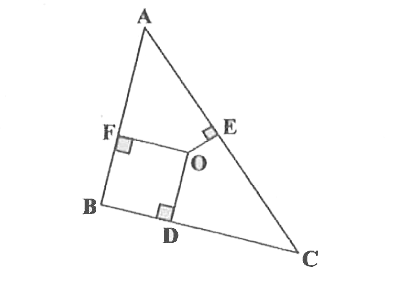
In fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
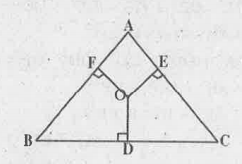
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన OA2+OB2+OC2−OD2−OE2−OE2=AE2+BD2+CE2
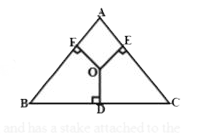
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
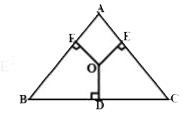
View SolutionIn the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
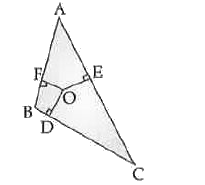
View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2.
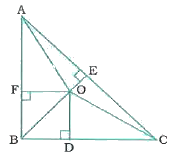
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2 .
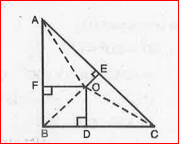
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- AF2+BD2+CE2=AE2+CD2+BF2 .
 .
.
View Solution
