In Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90o−12∠BAC.
Step by step video & image solution for In Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that /_B O C=90o-1/2/_B A C. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
आकृति 6.38 में, ΔABC की भुजाओं AB और AC को क्रमश : E और D तक बढ़ाया गया है | यदि ∠CBE और BCD के समद्विभाजक क्रमश : BO और CO बिंदु O पर मिलते है, तो सिद्ध कीजिए की ∠BOC=90∘−12∠BAC है |

View SolutionIn the adjacent figure BE⊥ DA and CD⊥DA then prove that m∠1≅m∠3.
View SolutionIn adjacent figure, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC<∠QCB. Show that AC > AB.

View SolutionIn the adjacent figure the sides AB and AC of ΔABCare produced to points E and D respectively. If bisectors BO and CO of ∠CBE and ∠BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC.
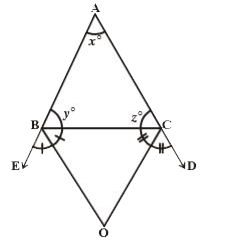
View SolutionIn the adjacent figure the sides AB and AC of ΔABCare produced to points E and D respectively. If bisectors BO and CO of ∠CBE and ∠BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC.

View SolutionIn Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that ∠BOC=90∘−12∠BAC.
View SolutionThe side BC of a triangle ABC is bisected at D;O is any point in AD.BOandCO produced meet ACandAB in EandF respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE∣∣BC.
View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
View Solution
