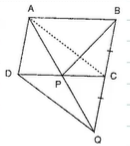
In Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD. Figure
Step by step video solution for In Figure, A B C D is a parallelogram and /_D A B=60^0dot If the bisectors A P and B P of angles A and B respectively, meet at P on C D , prove that P is the mid-point of C Ddot Figure by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:NCERT SECTION (Exercise 8.1 )
Explore 20 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:NCERT SECTION (Exercise 8.2 )
Explore 11 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:Olympiad/HOTS CORNER
Explore 15 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
In Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
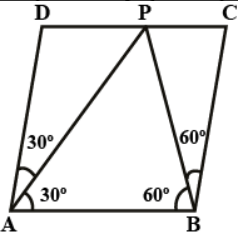
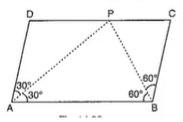
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD.
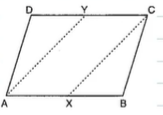
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
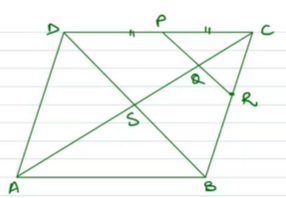
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
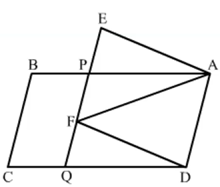
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View Solution