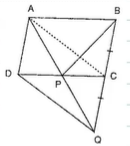
In Figure, ABC is an isosceles triangle in which AB=AC.andCP∣∣AB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
Step by step video & image solution for In Figure, A B C is an isosceles triangle in which A B=A Cdot and C P||A B and A P is the bisector of exterior /_C A D of A B C . Prove that /_P A C=/_B C A and (ii) A B C P is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
1000 families with 2 children were selected randomly and the following data were recorded.
∣∣∣Number of boys in a family 0 1 2Number of families 140 560 300∣∣∣
If a family is chosen at random, find the probability that it has
(i) no boy
(ii) one boy
(iii) two boys
(iv) at least one boy
(v) at most one boy.
View SolutionIf x=3+√8 , find the value of x2+1x2
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View SolutionBD and CE are bisectors of ∠B and ∠C of an isosceles ABC with AB=AC. Prove that BD=CE.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionIn Figure, ABCD is a parallelogram in which ∠A=600 . If the bisectors of ∠A and ∠B meet at P, prove that AD=DP,PC=BC and DC=2AD. Figure
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionBO and CO are respectively the bisectors of ∠B and ∠C of ABC . AO produced meets BC at P . Show that: ABBP=AOOP (ii) ACCP=AOOP (iii) ABAC=BPPC (iv) AP is the bisector of ∠BAC .
View SolutionIn a triangle ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q . Prove that ∠BPC+ ∠BQC=1800
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View Solution
