In Figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
Given ΔABC is an isosceles triangle in which AC=BC,AD and BE are respectively two altitude to sides BC and AC respectively
To Prove AE=BD
Proof in ΔABC AC=BC [given ]
∠ABC=∠CAB
[angles opposite to equal sides are equal ]
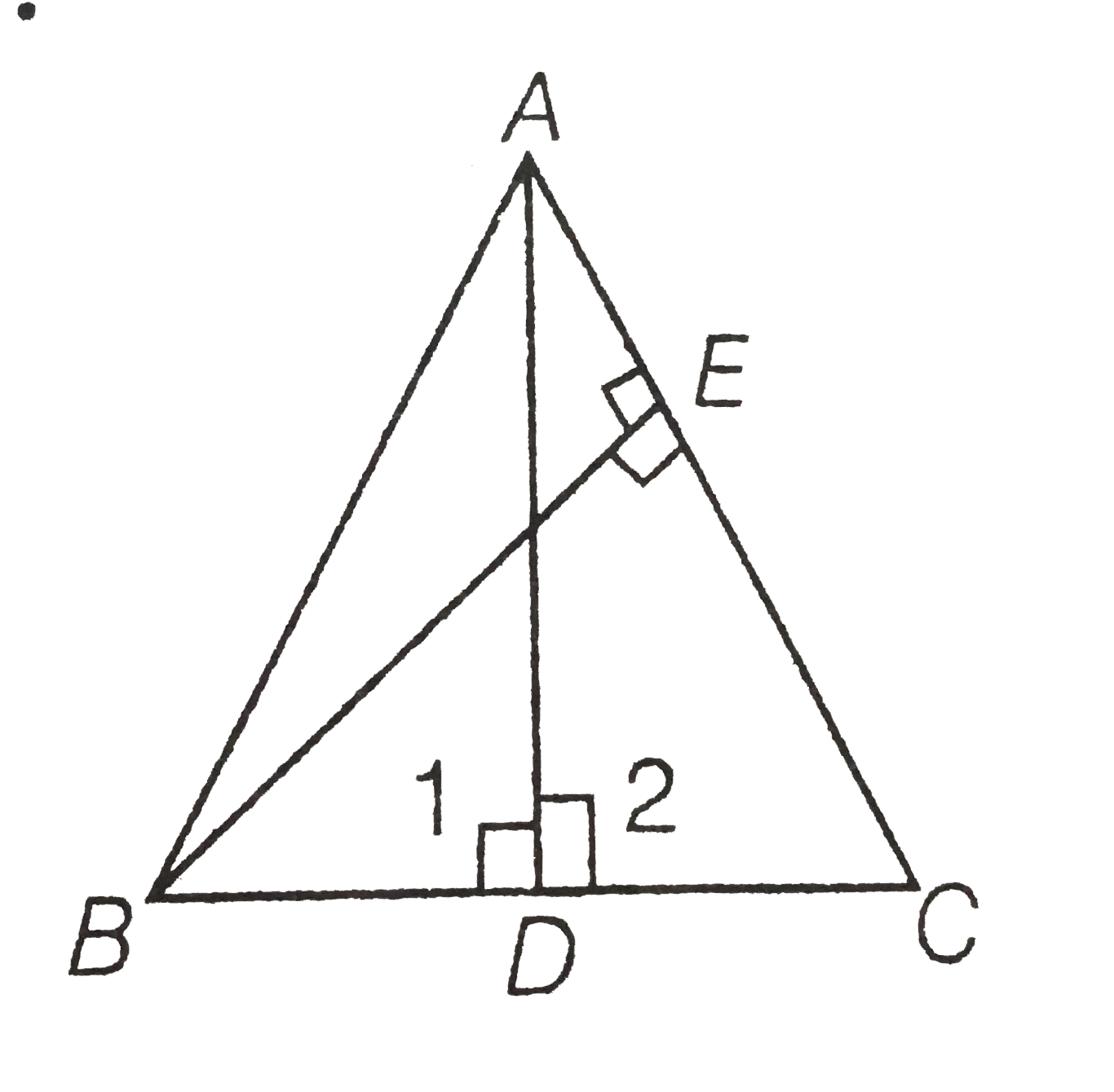
∠ABD=∠EAB
in ΔAEBandΔBDA,
∠AEB=∠ADB=90∘[ given ,AD⊥BC and BE⊥AC]
∠EAB=∠ABD [ from E q,(i) ]
and AB=AB [common side ]
∴ΔAEB≅ΔBDA [by AAS congruence rule ]
⇒ AE=BD [by CPCT ]
Topper's Solved these Questions
Similar Questions
The marks obtained by 40 students of class VIII in an examination are given below: 16,17,18,3,7,23,18,13,10,21,7,1,13,21,13,15,19,24,16,3, 23,5,12,18,8,12,6,8,16,5,3,5,0,7,9,12,20,10,2,23 Divide the data into five groups, namely 0-5, 5-10, 10-15, 15-20 and 20-25 and prepare a grouped frequency table.
View SolutionIf D and E are points on sides AB and AC respectively of a triangle ABC such that DE∣∣BC and BD=CE . Prove that ABC is isosceles.
View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
View SolutionIn Figure, AC=BC, ∠DCA=∠ECB and ∠DBC=EAC. Prove that triangle DBC and EAC are congruent, and hence DC=EC and BD=AE
View SolutionIn Figure, it is given that ∠A=∠C and AB=BC. Prove that ABD ≅CBE
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
View Solution
