In figure ∠ABD=∠ACD,AD is bisectyor of ∠BACandAD meets BC at D. Prove that D is mid-point of BC.
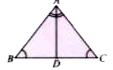
Step by step video solution for In figure angleABD=angleACD, AD is bisectyor of angleBAC and AD meets BC at D. Prove that D is mid-point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that ΔABC is isosceles if median AD is perpendicular to BC.
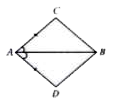
View SolutionIn quadrilateral ABCD, AC=AD and AB bisects ∠A (see figure). Show that ΔABC≅ΔABD. What can you say about BC and BD ?
View SolutionThe weight (in kg) of 50 students are given below
40 45 55 62 50 51 56 69 61 36
60 56 69 38 35 63 57 50 57 48
40 63 53 64 47 42 56 51 42 60
55 39 64 57 64 44 66 35 59 59
73 62 49 63 37 63 54 72 44 60
Find the mean, median and mode respectively for the given data.
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View Solution
