In Figure, if lines PQ and RS intersect at a point T such that ∠PRT=40∘, ∠RPT=95∘and ∠TSQ=75∘, find ∠SQT.
To solve the problem step by step, we will use the properties of angles in triangles and the concept of vertically opposite angles.
Step 1: Identify the angles given in the problem.
We have:
- Angle PRT = 40°
- Angle RPT = 95°
- Angle TSQ = 75°
Step 2: Find angle PTR in triangle RPT.
Using the property that the sum of angles in a triangle is 180°, we can write the equation for triangle RPT:
Angle PRT+Angle RPT+Angle PTR=180°
Substituting the known values:
40°+95°+Angle PTR=180°
Calculating the sum of the known angles:
135°+Angle PTR=180°
Now, isolate Angle PTR:
Angle PTR=180°−135°=45°
Step 3: Find angle STQ using vertically opposite angles.
Since angle STQ is vertically opposite to angle PTR, we have:
Angle STQ=Angle PTR=45°
Step 4: Find angle TQS in triangle STQ.
Now, we apply the sum of angles in triangle STQ:
Angle STQ+Angle TQS+Angle TSQ=180°
Substituting the known values:
45°+Angle TQS+75°=180°
Calculating the sum of the known angles:
120°+Angle TQS=180°
Now, isolate Angle TQS:
Angle TQS=180°−120°=60°
Step 5: Find angle SQT.
Since angle SQT is equal to angle TQS, we have:
Angle SQT=Angle TQS=60°
Final Answer:
Angle SQT=60°
---
We have:
- Angle PRT = 40°
- Angle RPT = 95°
- Angle TSQ = 75°
Using the property that the sum of angles in a triangle is 180°, we can write the equation for triangle RPT:
Angle PRT+Angle RPT+Angle PTR=180°
Substituting the known values:
40°+95°+Angle PTR=180°
Calculating the sum of the known angles:
135°+Angle PTR=180°
Now, isolate Angle PTR:
Angle PTR=180°−135°=45°
Since angle STQ is vertically opposite to angle PTR, we have:
Angle STQ=Angle PTR=45°
Now, we apply the sum of angles in triangle STQ:
Angle STQ+Angle TQS+Angle TSQ=180°
Substituting the known values:
45°+Angle TQS+75°=180°
Calculating the sum of the known angles:
120°+Angle TQS=180°
Now, isolate Angle TQS:
Angle TQS=180°−120°=60°
Since angle SQT is equal to angle TQS, we have:
Angle SQT=Angle TQS=60°
Angle SQT=60°
Topper's Solved these Questions
Similar Questions
From a discrete frequency distribution from the following scores: 15,18,16,20,25,24,25,20,16,15,18,18,16,24,15,20,28,30,27,16,24, 25,20,18,28,27,25,24,24,18,18,25,20,16,15,20,27,28,29,16
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

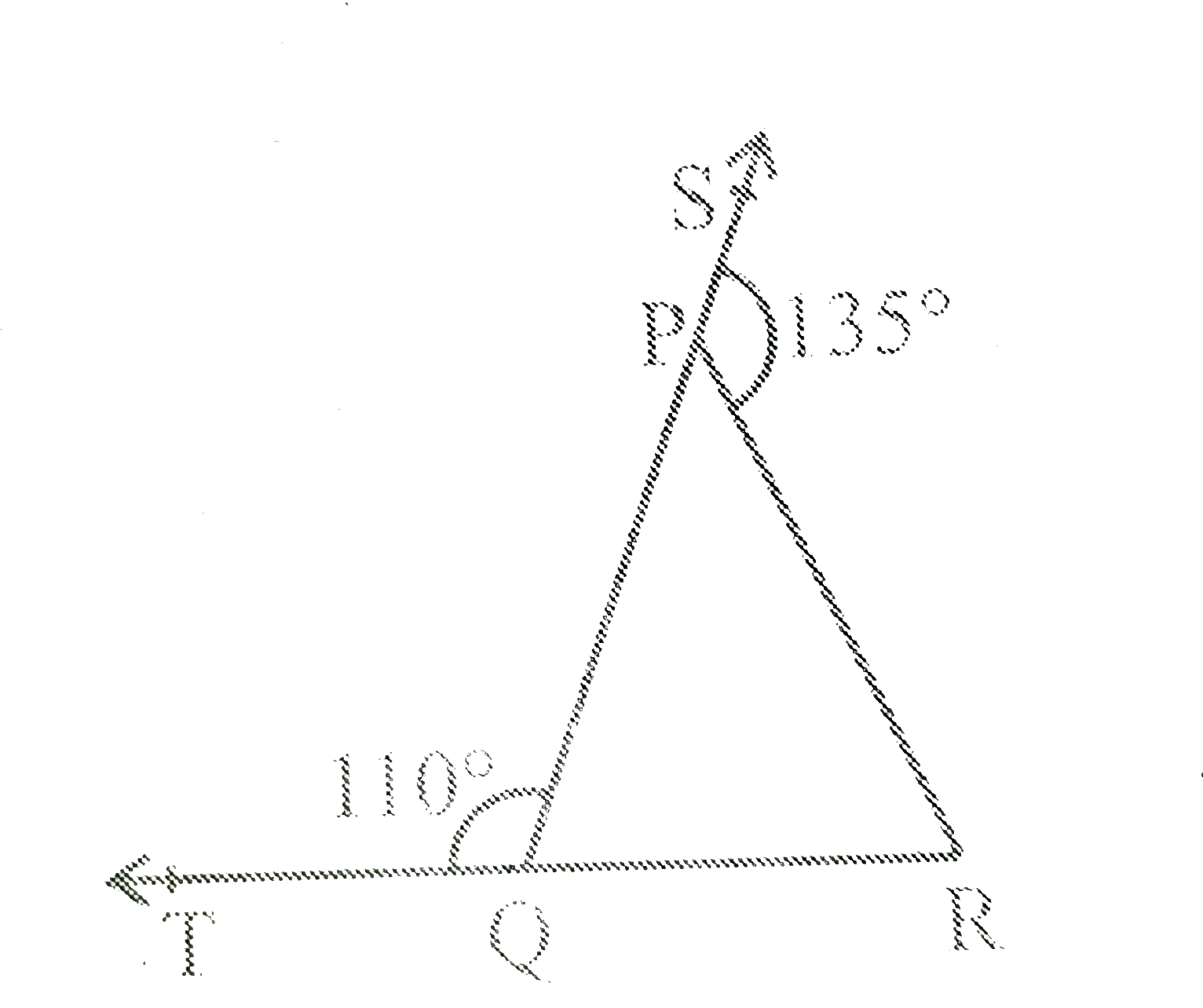
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIn Fig. 6.37, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find x and y.
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.

View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIn Figure PSSQ=PTTRand ∠PST=∠PRQ. Prove that PQR is an isosceles triangle.
View SolutionIn figure, if lines PQ and RS intersect at a point T such that PRT=400,∠RPT=950 and ∠TSQ=750, find ∠SQT. Figure
View Solutionsides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionIn Fig. 4.33, PSSQ=PTTR and ∠PST=∠PRQ . Prove that PQR is an isosceles triangle. (FIGURE)
View SolutionIn Fig. 4.99, if ∠P=∠RTS , prove that RPQ~RTS . (FIGURE)
View SolutionIn Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
View SolutionIn Figure, if QT⊥PR, ∠TQR=40∘ and ∠SPR=30∘, find x and y.
View Solution