In linear inequations, the set, from which the value of the variable x is to be chosen is called the replacement set and its subset, whose elements satisfy given inequation, is called the solution set of the linear inequation. Given A={x:5x−4≥6,x∈R}andB={x:5−x>1,x∈R}.
Answer the following questions:
The solution set of A on the number line is:


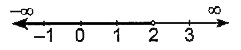
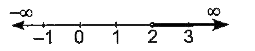
The correct Answer is:B
Topper's Solved these Questions
- LINEAR INEQUATIONSBook:ICSEChapter:LINEAR INEQUATIONSExercise:Assertion and Reason Based Questions
Explore 5 Videos
- HEIGHTS AND DISTANCES Book:ICSEChapter:HEIGHTS AND DISTANCES Exercise:Exercise 22 C
Explore 28 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)Book:ICSEChapter:LOCI (LOCUS AND ITS CONSTRUCTIONS)Exercise:EXERCISE 16(B)
Explore 49 Videos
Similar Questions
Assertion :If the solution set of 5x + 4≤24 is {1,2,3,4}, then the replacement set of x is N.
Reason: In number system, the symbol N denotes the set of natural numbers i.e., 1, 2, 3, 4, 5,6.....
View SolutionFind AD
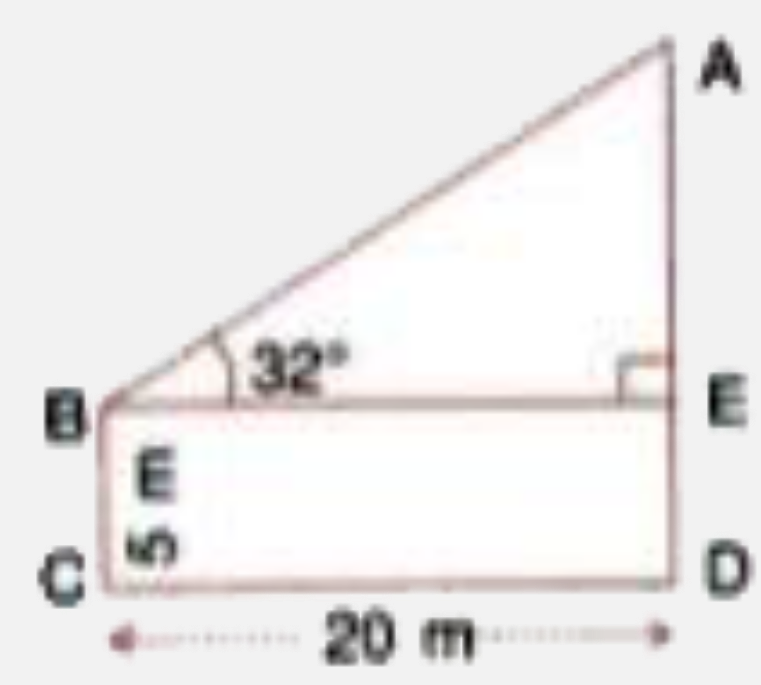
View SolutionThe locus of a point at a distance 3 cm from a fixed point.
View SolutionThe linear inequality representing the solution set given in gig. 15.44 is a. |x|<5 b. |x|>5 c. |x|≥5 d. |x|≤5
View SolutionFind the graph of linear inequation in xy plane y+2≤0
View SolutionFind the graph of linear inequation in xy plane x−2≤0
View SolutionFind the graph of linear inequation in xy plane x+4>0
View SolutionFind the graph of linear inequation in xy plane 2x−1≥0
View SolutionSolution set of inequality |x−1|<−1 is set R .
View SolutionSolution set of inequality |x−1|<−1 is set R .
View SolutionThe solution set of system of linear inequalities 2(x+1)≤x+5,3(x+2)>2−x,x∈R is
View SolutionSolution set of the inequation x−4x+1≥2 is
View SolutionIf
 is the solution set of a linear inequation in x, then the solution set of x in set-builder form is:
is the solution set of a linear inequation in x, then the solution set of x in set-builder form is:
View SolutionIf
 represents solution set of a linear inequation in x, then the replacement set of x must be:
represents solution set of a linear inequation in x, then the replacement set of x must be:
View SolutionIf
 represents solution set of a linear inequation in x, then the replacement set of x must be:
represents solution set of a linear inequation in x, then the replacement set of x must be:
View Solution
