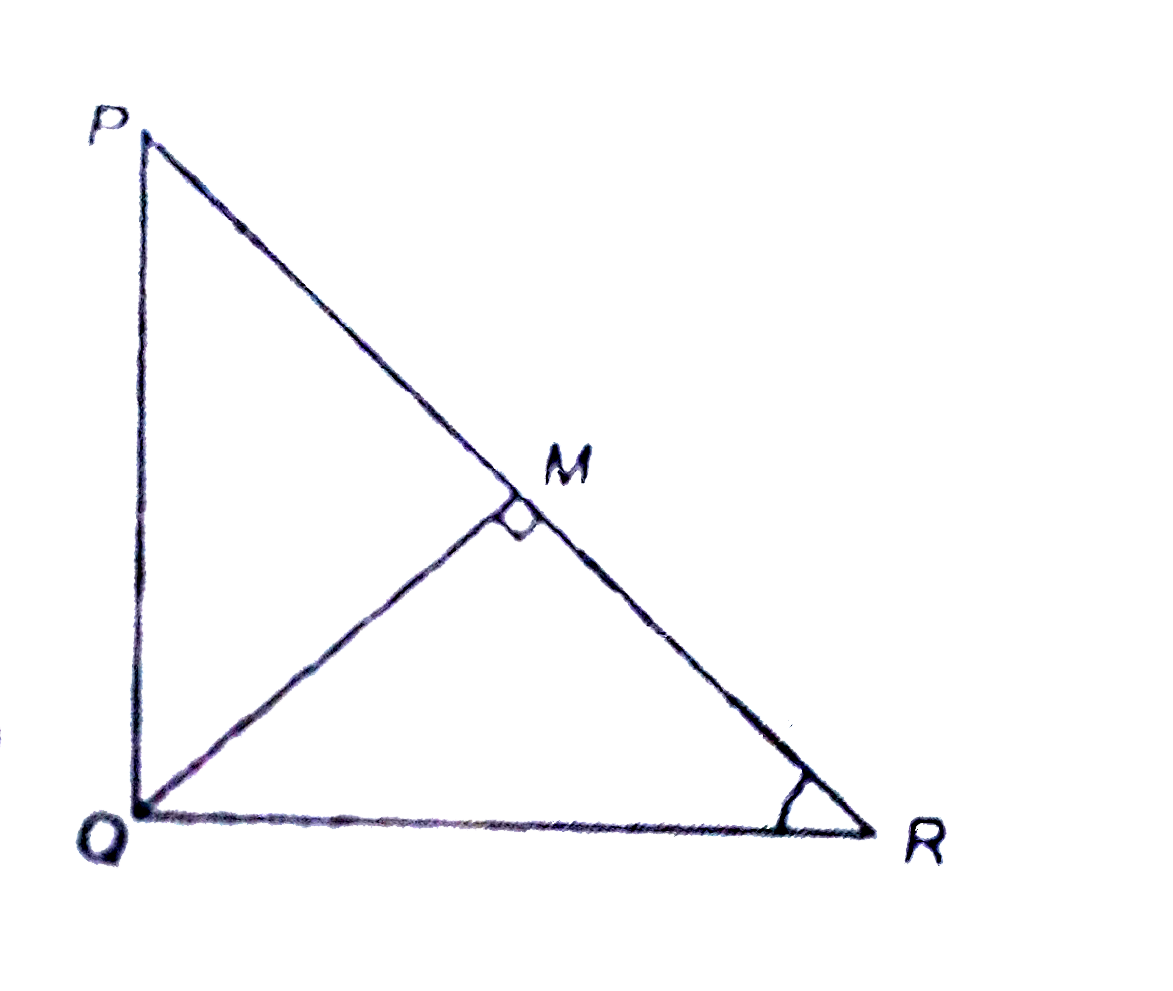
In PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
Given that
PR2−PQ2=QR2andQM⊥PR
PR2=PQ2+QR2
∠PQR=90∘ ( converse of Pythagoras theorem)
In △QMRand△PMQ
∠QMR=∠PMQ (each90∘))
∠MQR=∠MPQ (each90∘=∠R)
△QMR~∠PMQ (AA similarity)
⇒ area(△QMR)area(△PMQ)=QM2PM2
12×QM×RM12×QM×PM=QM2PM2
RM×PM=QM2
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6a
Explore 24 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Eercise 6b
Explore 1 Video
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 1 Video
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In Figure, it is given that LM=MN, QM=MR, ML ⊥PQ and MN ⊥PR. Prove that PQ=PR
View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Figure, PS=QR and ∠SPQ=∠RQP. Prove that PQS ≅ QPR, PR=QS and ∠QPR= ∠PQS
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionIn △PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MN∣∣QR .
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View Solution