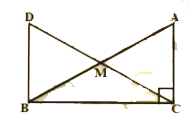
In right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB
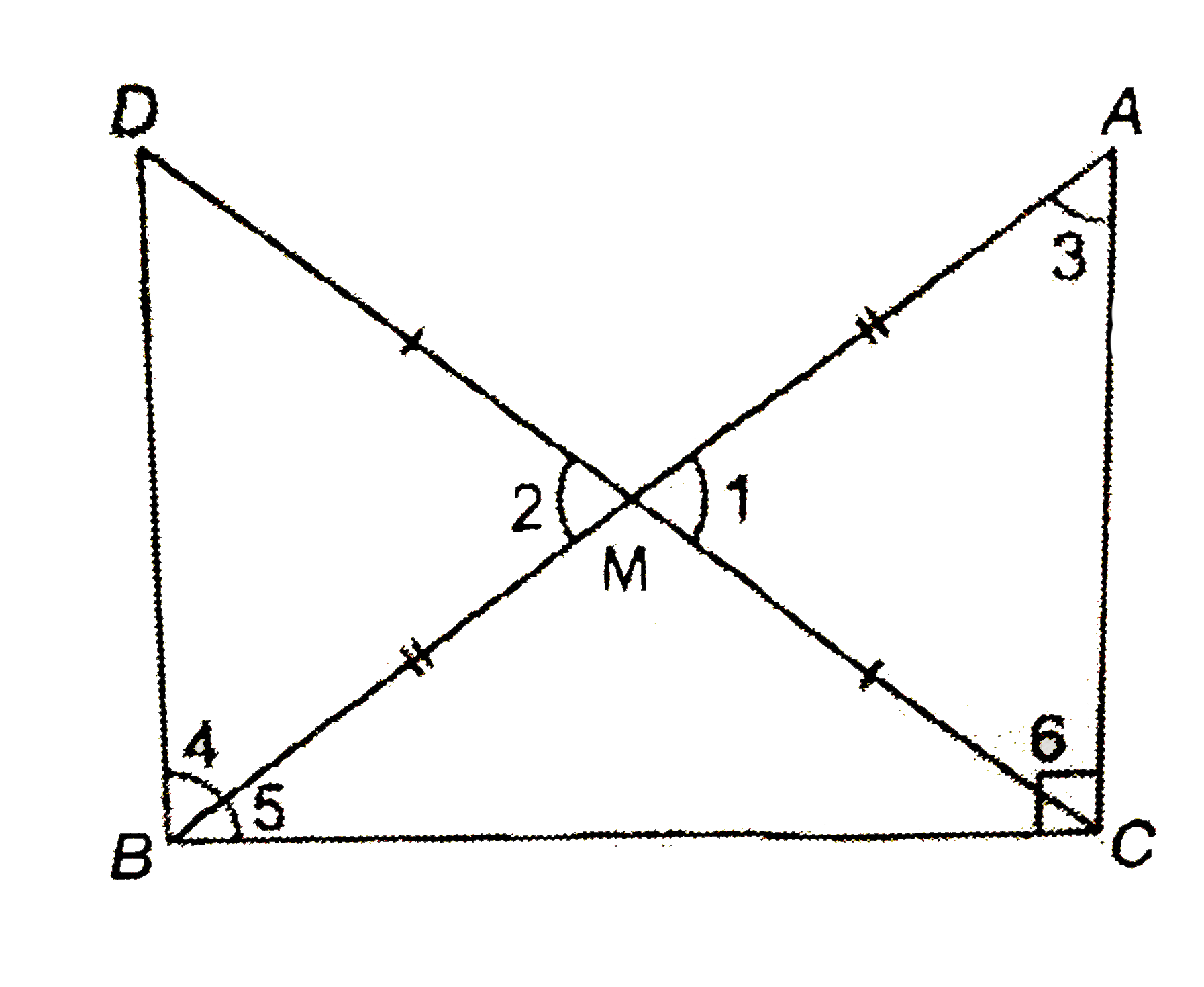
(i) In ΔAMC and ΔBMD,
∵⎧⎪⎨⎪⎩AM=BM(∵ M is the mid-point)∠1=∠2(vertically opposite angles)CM=DM(given)
∴ΔAMC≅ΔBMD (SAS)
⇒ AC=DB (c.p.c.t) ...(1) Hence Proved.
(ii) ∴∠3=∠4 (c.p.c.t.)
But these are the alternate angles which are equal.
∴AC∣∣BD
∴(∠4+∠5)+∠6=180∘ (sum of co-int ∠5 angles)
⇒ ∠4+∠5=180∘−90∘ (∵∠6=90∘, given)
⇒ ∠4+∠5=90∘
⇒ ∠DBC=90∘=∠ACB Hence Proved.
(iii) In ΔDBC and ΔACB,
∵⎧⎪⎨⎪⎩DB=AC[from (1)]∠DBC=∠ACB(just proved)BC=BC(common)
∴ΔDBC≅ΔACB (ASA) Hence Proved.
(iv) DC=AB (c.p.c.t)
⇒ 2CM=AB (∵ M is the mid-point of DC)
⇒ CM=12AB. Hence Proved.
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHAN ENGLISHChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
If 3 sides of a triangle are 35 cm, 16 cm and 12 cm, then which type of triangle is this ?
View SolutionWhich of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In ΔABC and ΔDEF,AB=EF,BC=DF and ∠B=∠F
(v) In ΔABC and ΔPQR,AB=QR,AC=PR and ∠B=∠R
(vi) In ΔABC and ΔPQR,∠A=∠P,AC=PR and AB=PQ
(vi) In ΔABC and ΔPQR,AB=QR,∠A=∠Q and AC=QP.
View SolutionHow many cubic metres of earth must be dug out to sink a well 14 m deep and having a radius of 4 m. If the earth taken out is spread over a plot of dimension (25m×16m). What is the height of the plateform so formed?
View SolutionIn right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB

View Solutionएक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है। दर्शाइए कि
(i) ΔAMC≅ΔBMD
(ii) ∠DBC एक समकोण है
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View Solutionएक समकोण त्रिभुज ABC में, C समकोण है, कर्ण AB का मध्य बिन्दु M है | C को M से मिलते हुए D तक इस प्रकार बढ़ाया गया है कि DM=CM है | बिन्दु D को बिन्दु B से मिलाया जाता है दर्शाइए कि
(i)ΔAMC≅ΔBMD
(ii)∠DBC=∠ACB=90∘
(iii)ΔDBC≅ΔACB
(iv)CM=12AB
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that
(i) △AMC≅△BMD
(ii) ∠DBC is a right angle.
(iii) △DBC≅△ACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
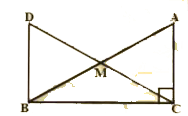
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
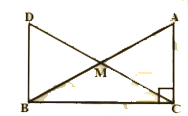
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
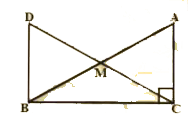
View Solutionएक समकोण त्रिभुज ABC में, जिसमे कोण C समकोण है, M कोण AB का मध्य बिन्दु है | C को M से मिलाकर D तक इस प्रकार भाधाया गया है कि DM -= CM है | बिन्दु D को बिन्दु B से मिला दिया जाता है ( देखिए आक्रति ) | दर्शाइए कि-
(i) ΔAMC ~-= ΔBMD
(ii) ∠DBC एक समकोण है |
(iii) ΔDBC ~-= ΔACB
(iv) CM -= 12AB
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.
) Show that : ΔAMC≅ΔBMD.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ∠DBC is a right angle.
) Show that : ∠DBC is a right angle.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔDBC≅ΔACB.
) Show that : ΔDBC≅ΔACB.
View Solution