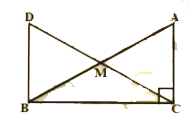
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.Solution in Punjabi
) Show that : ΔAMC≅ΔBMD.Solution in Punjabi
Step by step video solution for In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig. ) Show that : DeltaAMC ~= DeltaBMD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES Book:SWAN PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 7.2
Explore 10 Videos
- TRIANGLES Book:SWAN PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 7.3
Explore 10 Videos
- SURFACE AREAS AND VOLUMES Book:SWAN PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:Objective Type Questions (Fill in the Blanks )
Explore 7 Videos
Similar Questions
In an isosclees triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O show that : OB=OC.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
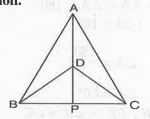 ).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.
View SolutionTotal surface area of a cone = ..............
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that
(i) △AMC≅△BMD
(ii) ∠DBC is a right angle.
(iii) △DBC≅△ACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
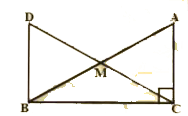
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
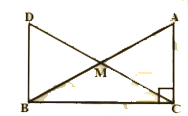
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
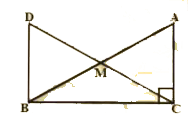
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
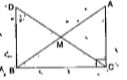
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.
) Show that : ΔAMC≅ΔBMD.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ∠DBC is a right angle.
) Show that : ∠DBC is a right angle.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔDBC≅ΔACB.
) Show that : ΔDBC≅ΔACB.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : CM=12AB.
) Show that : CM=12AB.
View SolutionIn right triangle ABC, right angle is at 'C'. M s the mid-point of hypotenuse . ABC is joined to M and produced to a point D such that DM = CM. Point D is Joined to point B (see fig.). Show that: CM=12AB
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.
) Show that : ΔAMC≅ΔBMD.
View Solution