In the 20 th row of the triangle

6/5
7/2
9/5
none of these
The correct Answer is:B
Let the first term be a and common difference be d for the first A.P. and the first term be b and common difference be e for the second A.P. and let the numbers of terms be n. Then
a+(n−1)db=b+(n−1)ea=4 (1)
n2[2a+(n−1)d]n2[2b+(n−1)e]=2 (2)
From (1) and (2), we get
a-4b+(n-1)d=0 (3)
b-4a+(n-1)e=0 (4)
2a-4b+(n-1)d-2(n-1)e=0 (5)
4×(3)+(4) gives
−15b+4(n−1)d+(n−1)e=0 (6)
(4)+2×(5) gives
−7b+2(n−1)d−3(n−1)e=0 (7)
Further, 15×(7)−7×(6) gives
2(n−1)d−52(n−1)e=0
or d=26e (∵n>1)
∴d/e=26
Putting d=26e in (3) and solving it with (4), we get
a=2(n-1)e,b=7(n-1)e
Then, the ratio of their nth terms is
2(n−1)+(n−1)26e7(n−1)e+(n−1)e=72
Topper's Solved these Questions
Similar Questions
Knowledge Check
Sum of all the terms in the nth row of the triangle
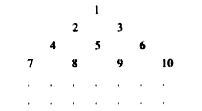 isA12n2(n+1)B12n(n2+1)Cn(n2+1)Dn2(n+1)
isA12n2(n+1)B12n(n2+1)Cn(n2+1)Dn2(n+1)The sum of the elements in the sixth row of Pascal triangle is ___________
A32B63C128D64If Ravindra finds that he is 20th from the right end in a row of boys and 6th from the left end, how many boys should be added to the row such that there are 36 boys in the row?
A12B11CCannot be determinedD13
What is the coefficient of a term in a row of Pscal triangle if in the preceding row, the coeficient on the immediate left is 5 on the immediate rigth is 10
View SolutionWhat is the 6th sicth entry in row 5 of pascle's triangle?
View SolutionWhat is the 6th sicth entry in row 5 of pascle's triangle?
View SolutionIn a row of trees , a tree is at 11 th place in the row from the left and 16 th place from the right .How many trees are there in this row ?
View SolutionSome identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of row balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then, the number of balls used to form the equilateral triangle is
View Solution

