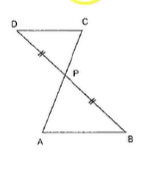
In the adjoining figure, ABCD is a ||gm in which P is the midpoint of DC and Q is a point on AC such that CQ=14AC. Also, PQ when produced meets BC at R. Prove that R is the midpoint of BC.
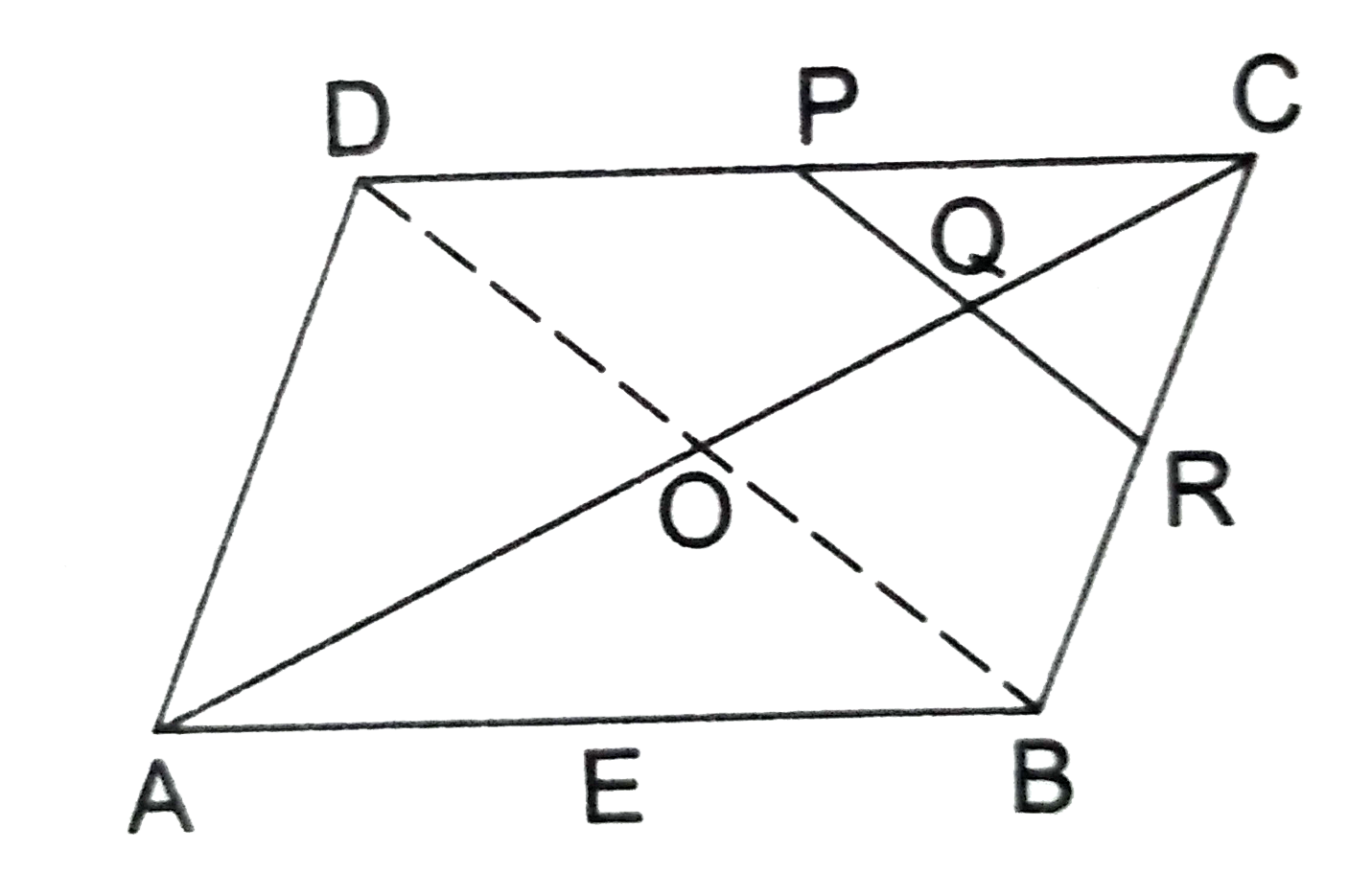
Join BD, intersecting AC at O.
Then, AO=OC [∵ diagonals of a ||gm bisect each other].
∴CQ=14AC=14×(2OC)=12OC.
Thus, Q is the midpoint of OC.
Now, in △CDO, P and Q are the midpoint of CD and CO respectively.
∴ PQ||DO and thererfore, QR||OB [∵ PQ||DO⇒ PQR||DOB].
Now, in △COB, Q is the midpoint of CO and QR||OB.
∴ R must be the midpoint of BC.
Similar Questions
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ =14AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.
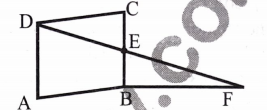
View SolutionIn the given figure, ABCD is a ||gm and E is the mid-point of BC. Also, DE and AB when produced meet at F. Then.
View Solution
Knowledge Check
ABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
ArectangleBsquareCparallelogramDrhombus
In the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
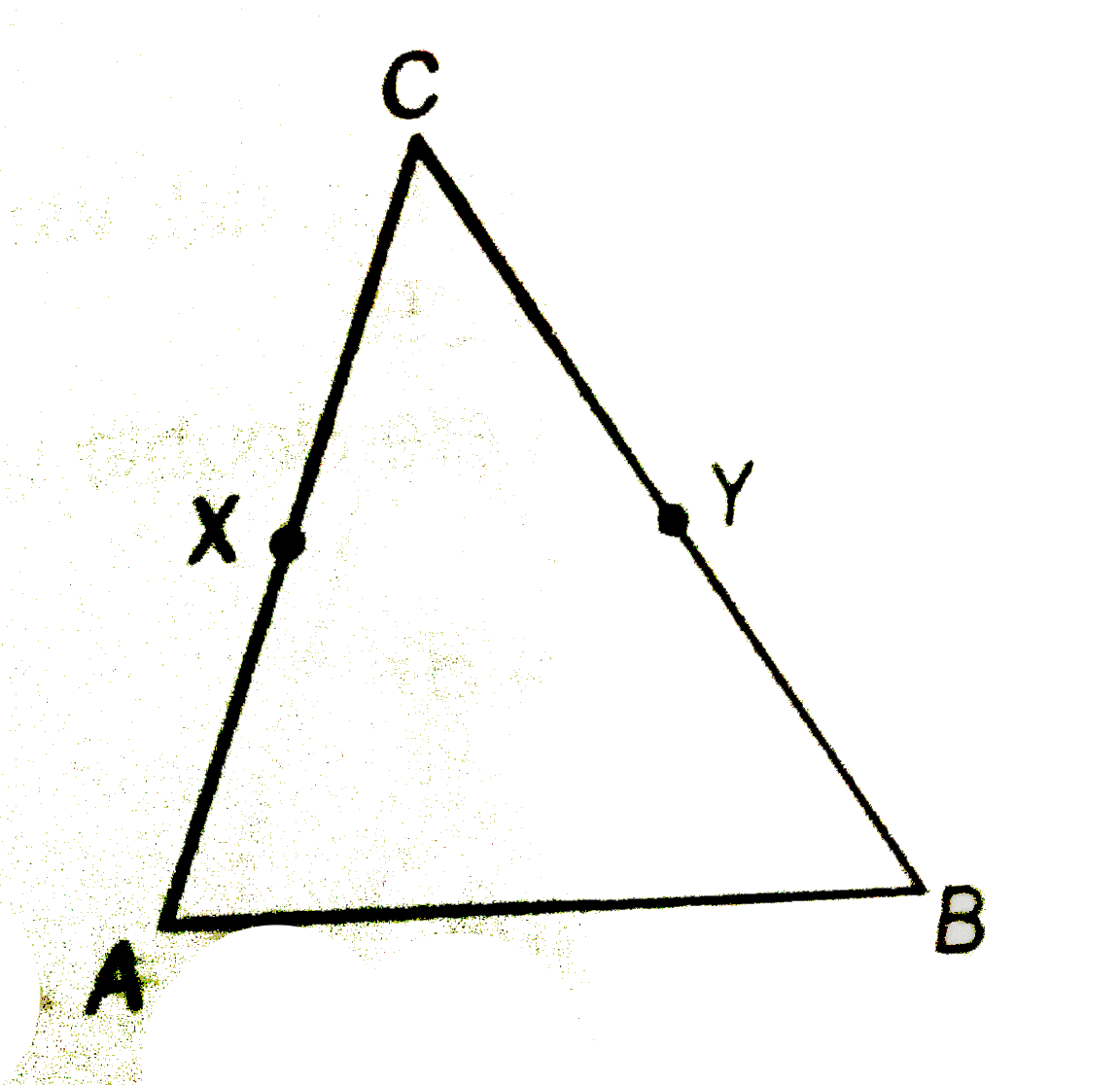
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
View SolutionIn Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionIn the adjoining figure PR||AB, PQ||BC and QR||AC. Then what is the relation between AC and QR?
View Solution
