In the adjoining figure, ABCD is a parallelogram and X, Y are the points on the diagonal BD such that DX = BY. Prove that
(i) CXAY is a parallelogram,
(ii) △ADX≅△CBYand△ABY≅△CDX,and
(iii) AX=CYandCX=AY.
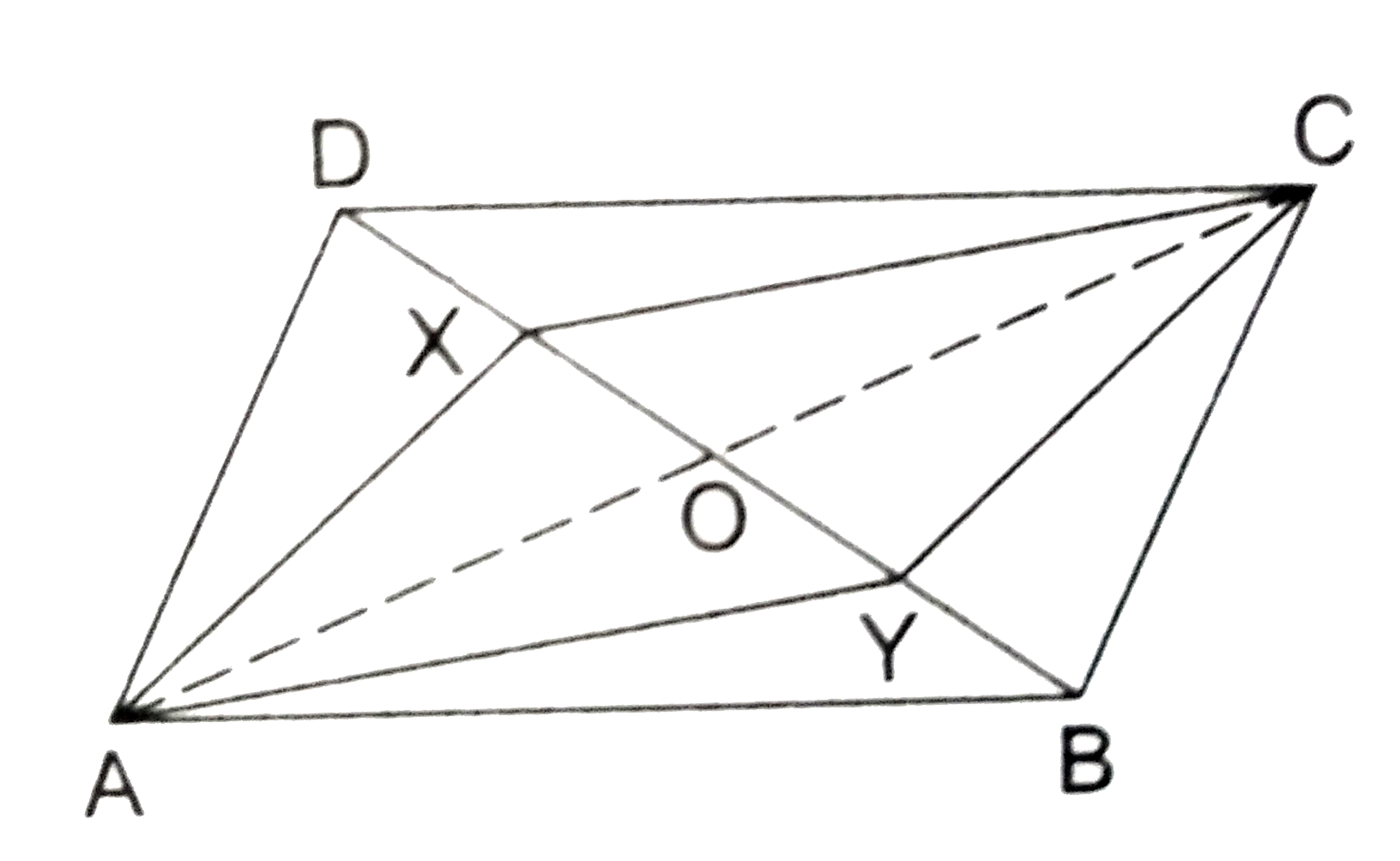
(i) Join AC , meeting BD at O.
Since the diagonals of a parallelogram bisect each other,
we have OA = OC and OD = OB.
Now, OD = OB and DX = BY
⇒OD−DX=OB−BY⇒OX=OY.
Now, OA = OC and OX = OY.
CXAY is a quadrilateral whose diagonals bisect each other.
∴CXAYisa∣∣gm.
(ii) and (iii) in △ADXandCBY, we have
AD=BC (opp. sides of a || gm)
∠ADX=∠CBY (alt. interior ∠)
DX=BY (given)
∴△ADX≅△CBY (SAS- criterion).
And so, AX=CY (c.p.c.t.).
Similarly, △ABY≅△CDX and so CX=AY(c.p.c.t.).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Three angles of a quadrilateral are 75∘,90∘and75∘. Find the measure of the fourth angle.
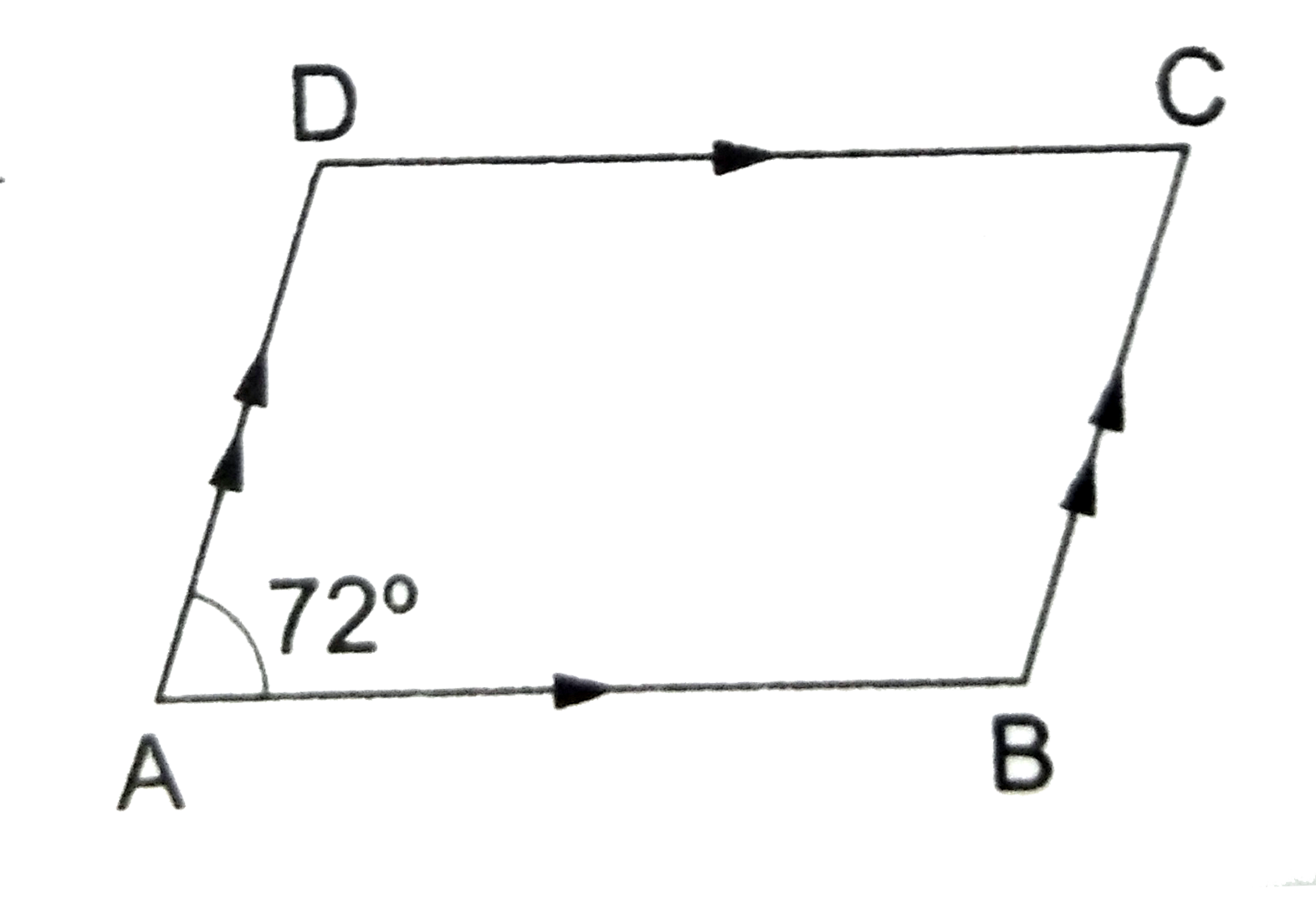
View SolutionIn the adjoining figure, ABCD is a parallelogram in which ∠A=72∘. Calculate ∠B,∠Cand∠D.
View SolutionMatch the following columns:
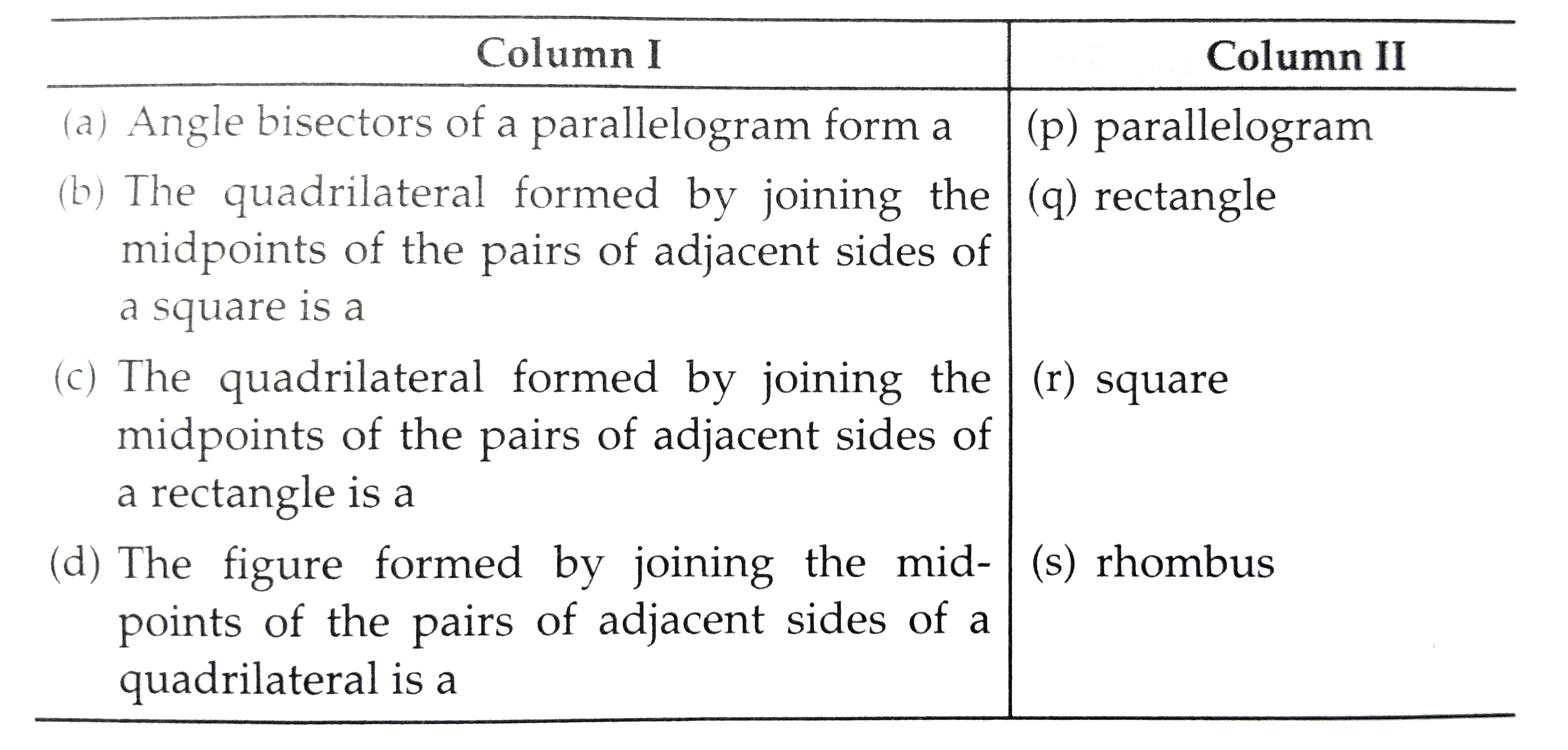
The correct answer is :
(a) - ……., (b) - ……., (c ) - ……., (d) - ………
View SolutionIn a sample survey of 645 people , it was found that 516 people have a high school certificate . If a person is chosen at random , what is the probability that he/she has a high school certificate ?
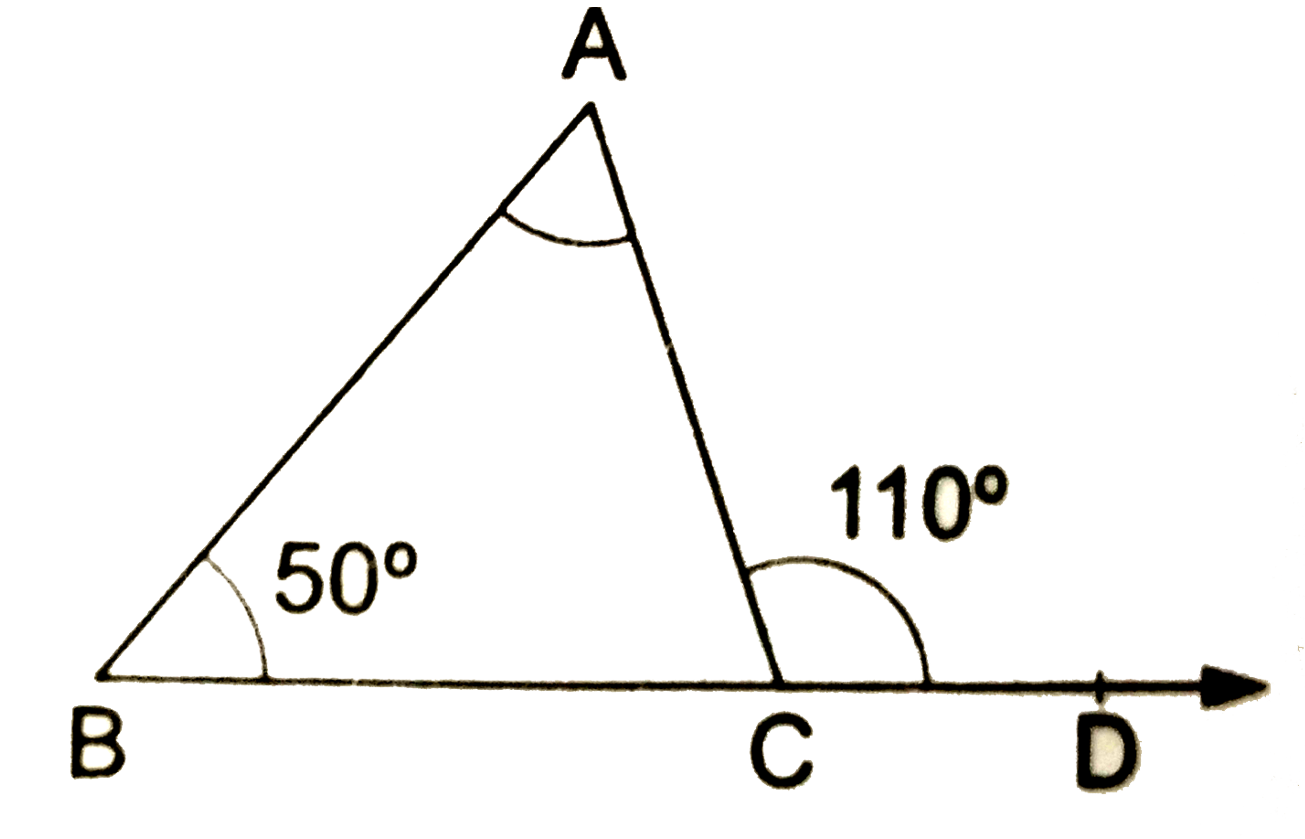
View SolutionIn a ΔABC, side BC is produced to D. If ∠ABC=50∘and∠ACD=110∘ then ∠A=?
View SolutionProve that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_VIII_C16_E04_031_Q01.png" width="80%"gt
(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionIn the following figure ,ABCD is a parallelogram, CB is extended to F and the line joining D and F intersect AB at E. Then prove that ΔEAD~ΔEBF
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, DEF is a triangle. If DF is the longest side and EF is the shortest side, then which of the following is true?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_028_Q01.png" width="80%"gt
View Solution