In the adjoining figure, ABCD is a parallelogram, E is midpoint of AB and CE bisects ∠BCD. Prove that
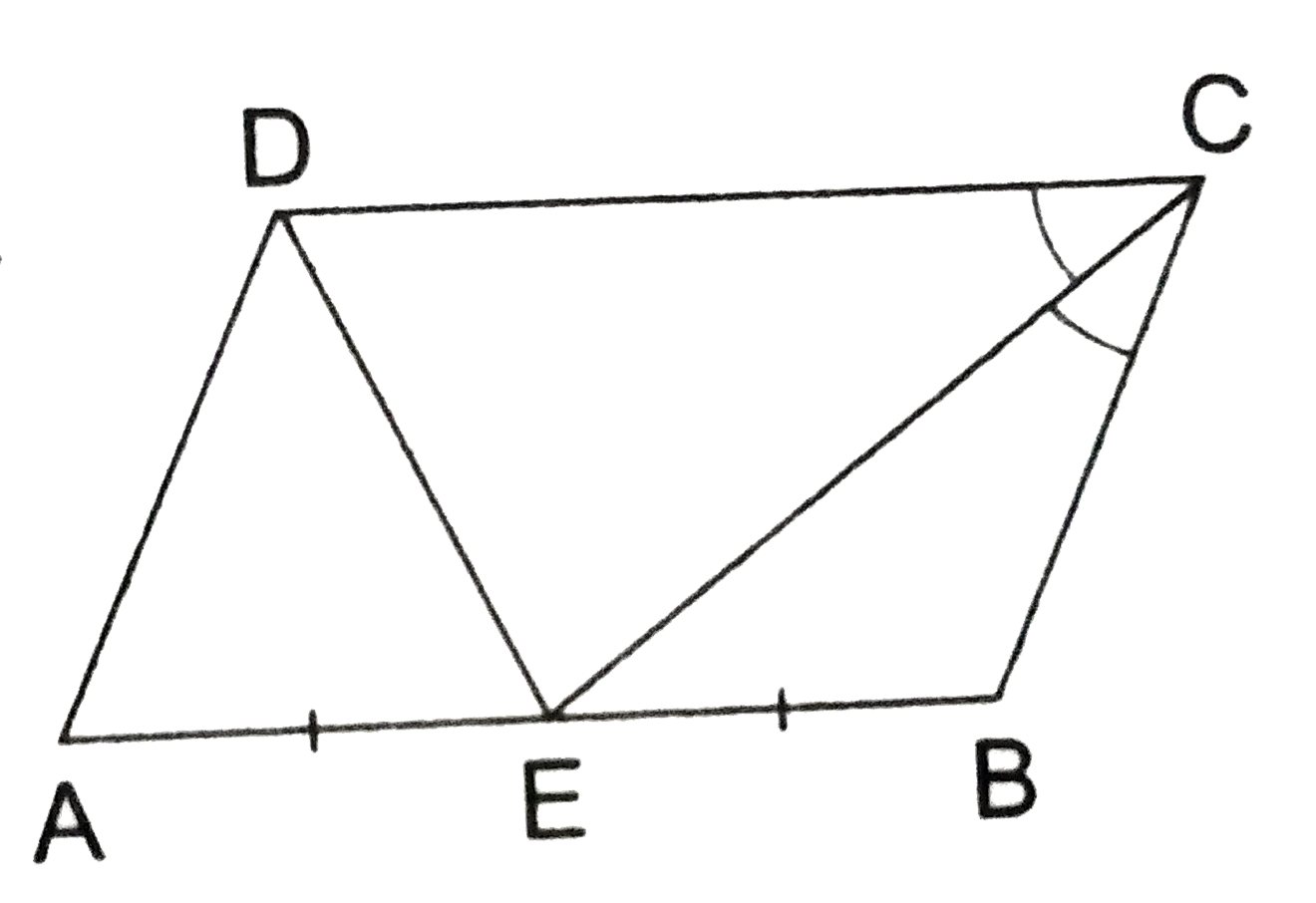
(i) AE = AD (ii) DE bisects ∠ADC and (iii) ∠DEC=90∘.
AB||DC and EC cuts them ⇒∠BEC=∠ECD
⇒∠BEC=∠ECB [∵∠ECD=∠ECD
⇒EB=BC⇒AE=AD.
Now, AE=BC⇒∠ADE=∠AED⇒∠ADE=∠EDC [∵∠AED=∠EDC( alt. interior ∠)].
∴ DE bisects ∠ADC.
Further , ∠ADC+∠BCD=180∘ [co-interior ∠]
⇒12∠ADC+12∠BCD=90∘⇒∠EDC+∠DCE=90∘.
But, ∠EDC+∠DCE+∠DEC=180∘ [sum of the ∠ of a △]
∴∠DEC=90∘.
Similar Questions
If ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Provethat:(i) AE=AD(i) DE bisects ∠ADC and(ili) Angle DEC is a right angle.
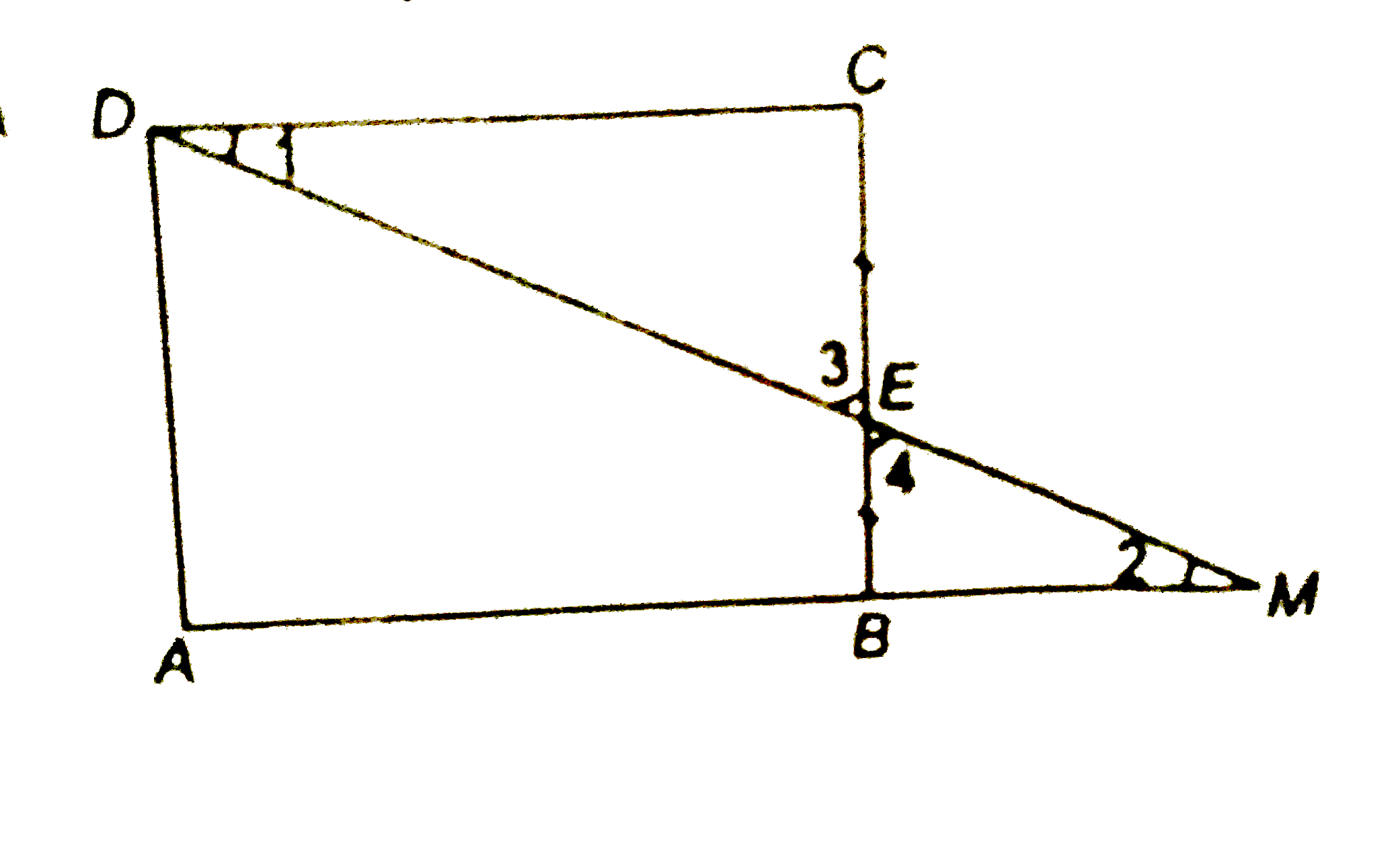
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
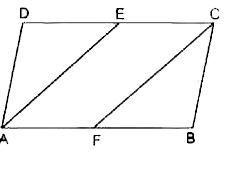
View SolutionIn the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionABCD is a parallelogram and bisector of angle A bisects BC at X. Show that AD= 2AB
View SolutionABCD is a parallelogram. AB is produced to E so that BE=AB . Prove that ED bisects BC.
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line Bcat point X. Prove that AD = 2AB.
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X. prove that AD=2AB.
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution