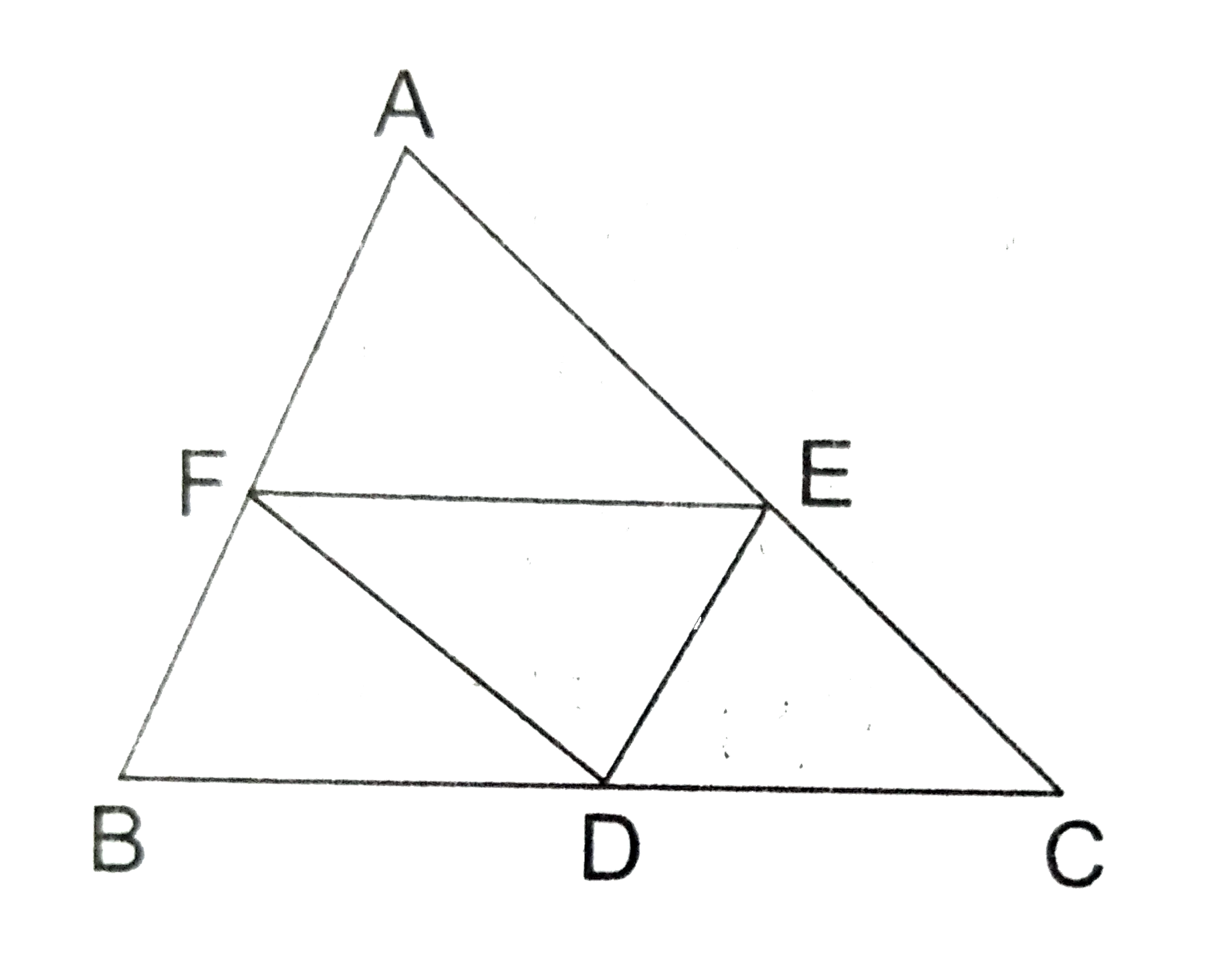
In the adjoining figure, D, E, F are the midpoints of the sides BC, CA and AB respectively, of △ABC. Show that ∠EDF=∠A,∠DEF=∠Band∠DFE=∠C.
Video Solution
Text Solution
DE||BA and DE=12BA⇒ DE||FA and DE = FA.
∴DEAF is a ||gm.
So, ∠EDF=∠A [opposite ∠ of a ||gm].
Similarly, ∠DEF=∠Band∠DFE=∠C.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 47 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 9 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
In right angled ΔABC,∠B=90∘, if P and Q are points on the sides AB and BC respectively, then :
 AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)
AAQ2+CP2=2(AC2+PQ2)BAQ2+CP2=AC2+PQ2C(AQ2+CP2)=12(AC2+PQ2)D(AQ+CP)=12(AC+PQ)In a ΔABC,∠C=3∠B=2(∠A+∠B), then ∠B = ?
A20∘B40∘C60∘D80∘BC, AB and AC are tangents to the circle at D, E and F respectively. ∠EBD=x∘,∠FCD=y∘. Then ∠ EDF equals
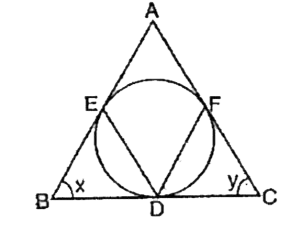 Ax + yBx2−yC90∘−(x+y)Dx+y2
Ax + yBx2−yC90∘−(x+y)Dx+y2
lf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionIn the given figure , D is a point on the side BC of ΔABC such that ∠ADC=∠BAC. Prove that CA2=CB×CD.
View SolutionIn ΔABC,MandN are points on the sides AB and AC respectively such that BM=CN. If ∠A=∠C then show that MN∣∣BC.
View SolutionIn a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionIn ΔABC, ∠A+∠B=65∘,∠B+∠C=140∘ then find ∠B.
View Solution
