In the adjoining figure, show that ∠A+∠B+∠C+∠D+∠E+∠F=360∘

Video Solution
Text Solution
Divide the whole figuer into two triangles, namely ΔDFBandΔEAC.
∴∠A+∠B+∠C+∠D+∠E+∠F
=(∠A+∠C+∠E)+(∠B+∠D+∠F)
=(180∘+180∘)=360∘.

|
Similar Questions
Knowledge Check
In figure, ∠B<∠Aand∠C<∠D then
 AAD<BCBOD>OCCOB<OADNone of these
AAD<BCBOD>OCCOB<OADNone of theseIn the formula ∠A+∠B+∠C=180∘, if ∠A=90∘ and ∠B=55∘, then ∠C=_______
A45∘B45∘C25∘D35∘In a △ABC if 3∠A=4∠B=6∠C,calculate ∠A
A∠A=60∘B∠A=80∘C∠A=40∘DNone of these
in the adjoining figure find ∠F.
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
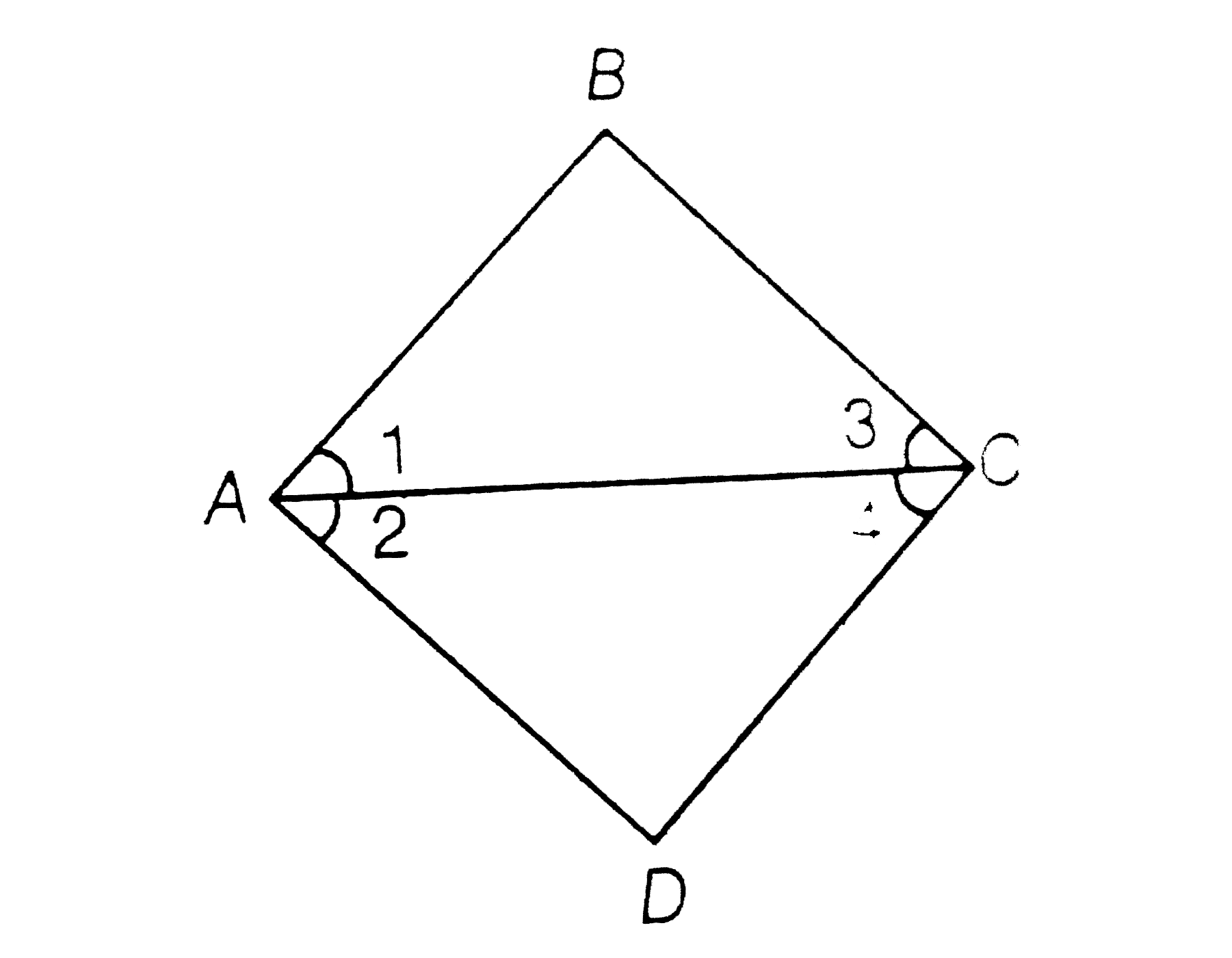
View SolutionIn the given figure we have ∠1=∠3and∠2=∠4 show that ∠A=∠C
View SolutionIf one angle of a triangle is equal to the sum of the other two,show that the traingle is right angled.
Hint.∠A=∠B+∠C⇒∠A+∠B+∠C+=180∘
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View Solution