In the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
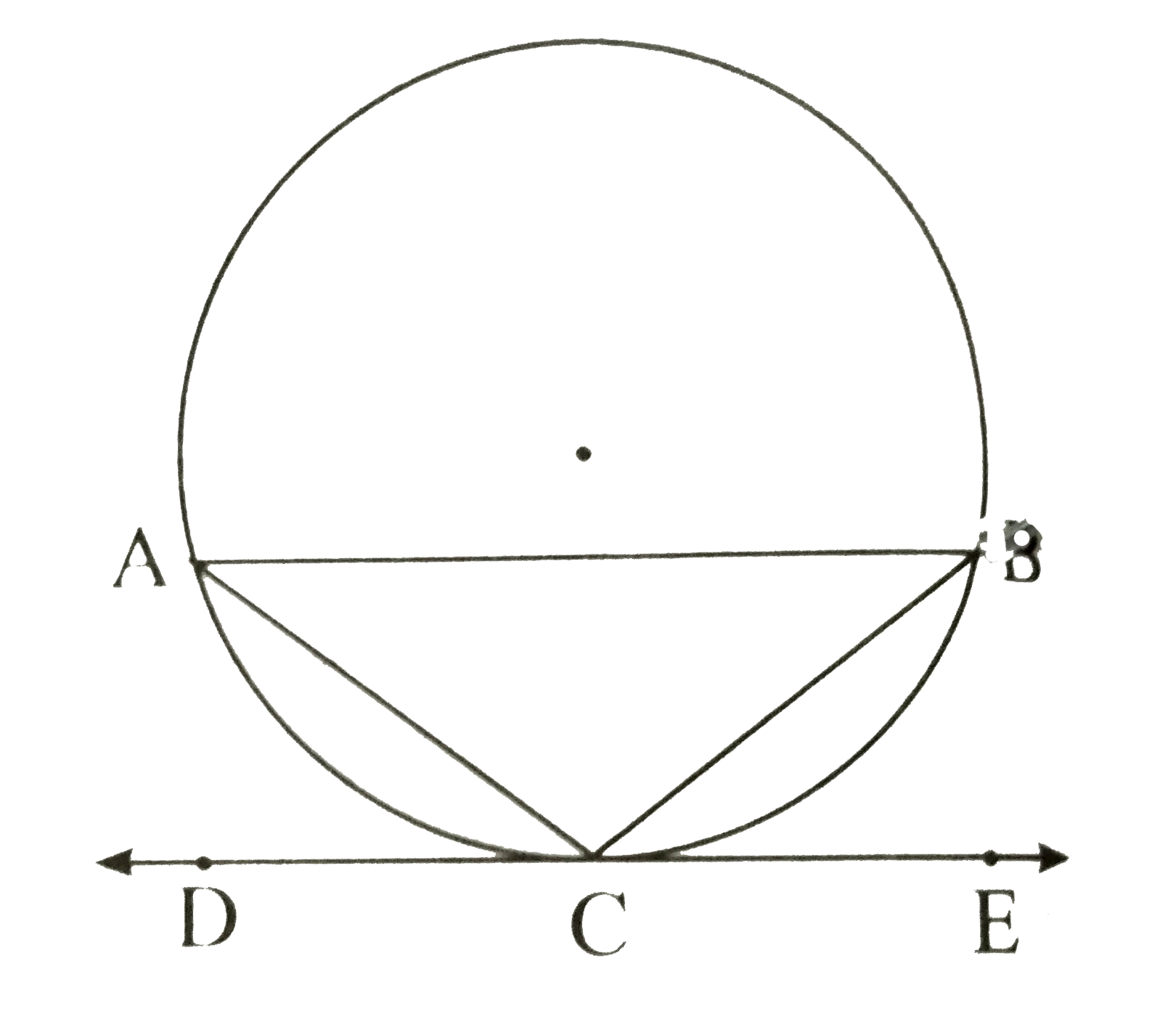
Seg AB∣∣line DE and line AC is the transversal,
∴∠BAC≅∠ACD …(Alternate angles ) …(1)
∠ACD≅∠ABC ….(Tangent decant theorem ) ….(2)
∴ from (1) and (2) , we get ,
∠BAC≅∠ABC
∴ seg AC≅∠ABC
∴ seg AC≅ seg BC ....(Converse of isosceles triangle theorem )
∴AC=BC
Similar Questions
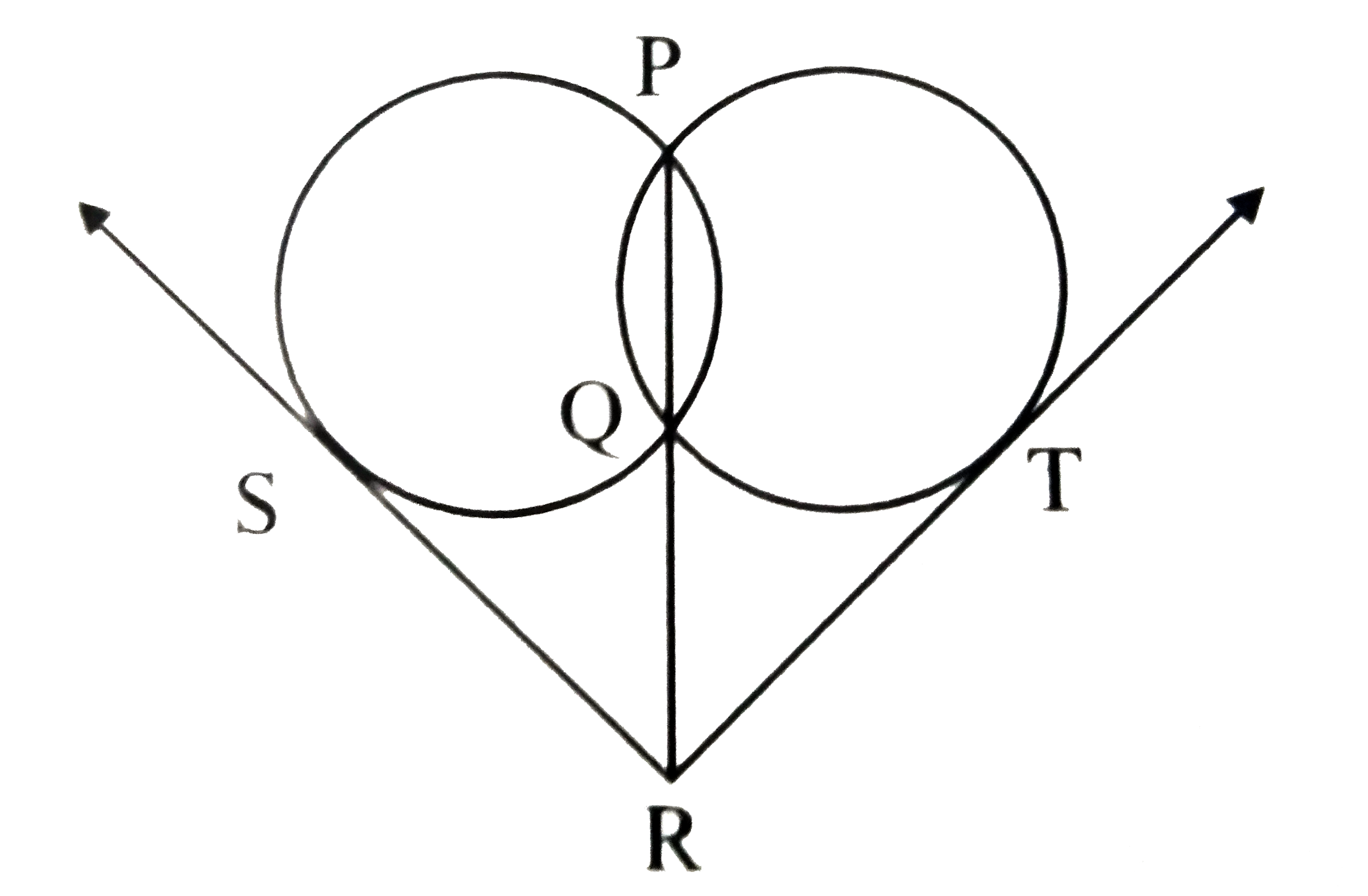
In the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
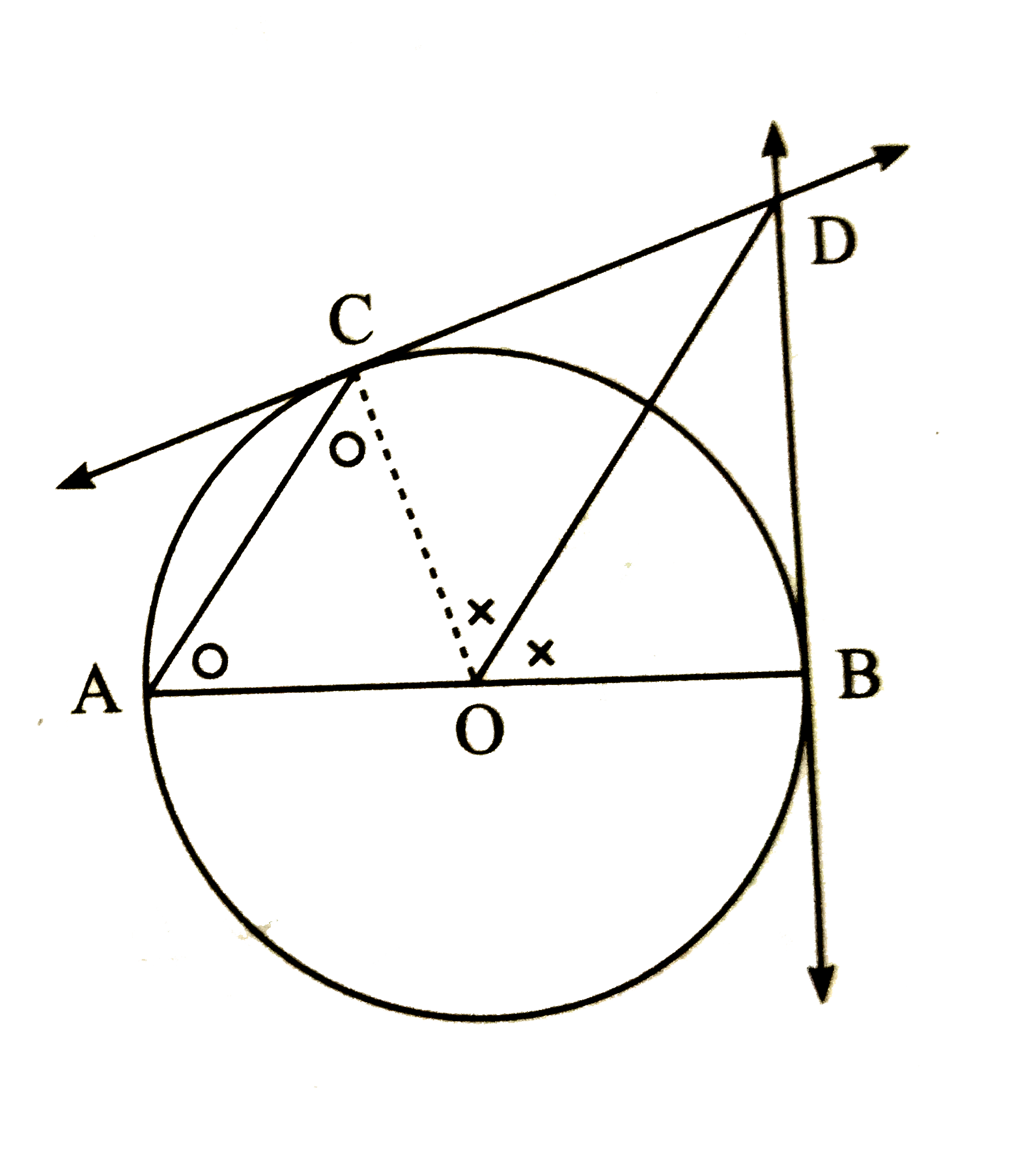
View Solution
Knowledge Check
In the figure , PQ and PT are tangents. AB is a third tangent touching the circle at C. If PQ = 35 cm , then the perimeter of ΔPAB is
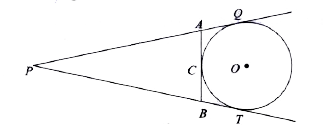 A70 cmB35√2 cmC35√3 cmD35 cm
A70 cmB35√2 cmC35√3 cmD35 cmIn the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
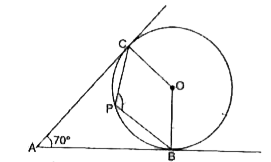 A110∘B140∘C125∘D136∘
A110∘B140∘C125∘D136∘In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
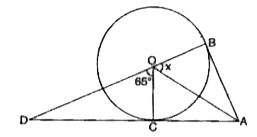 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
In the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
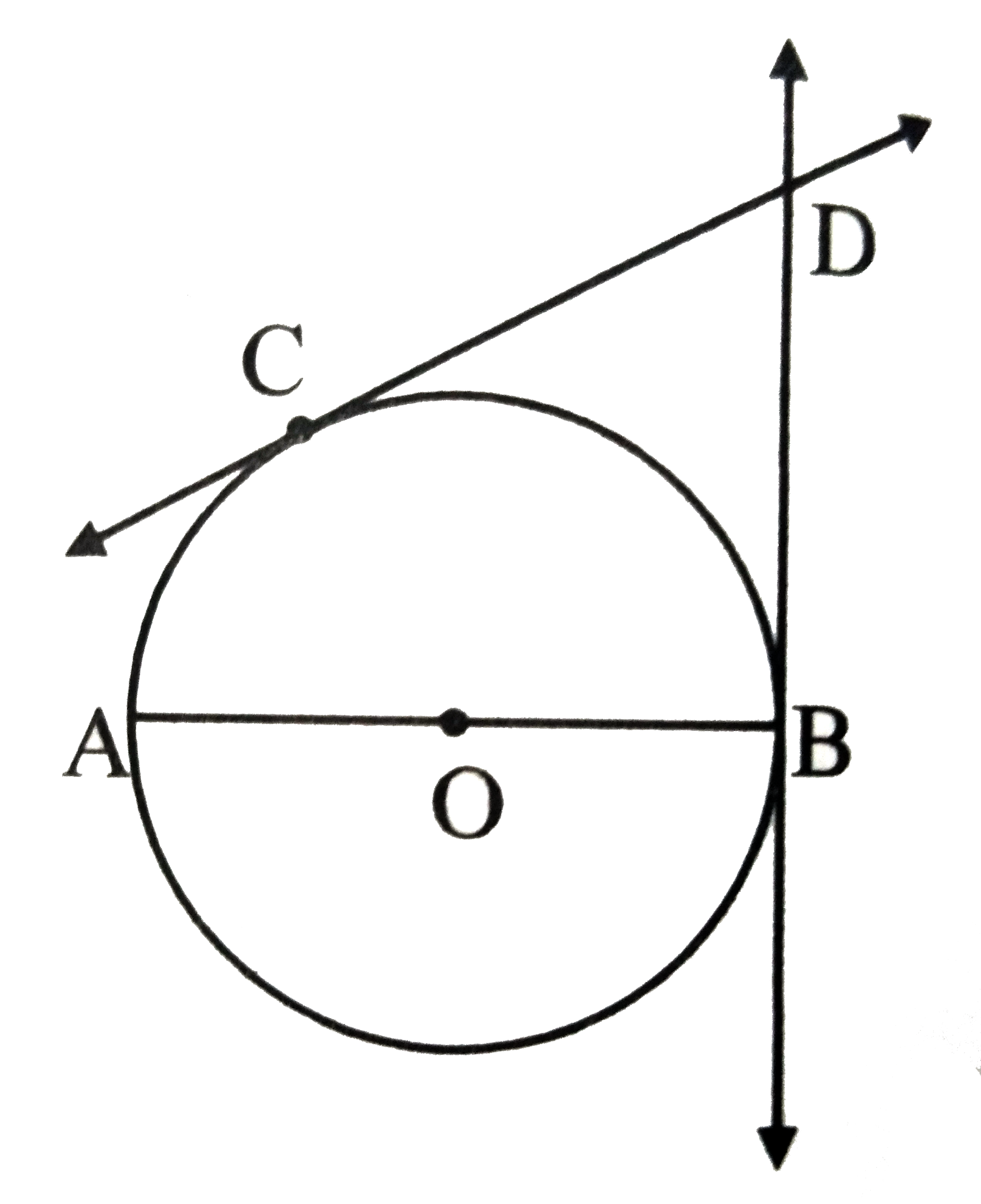
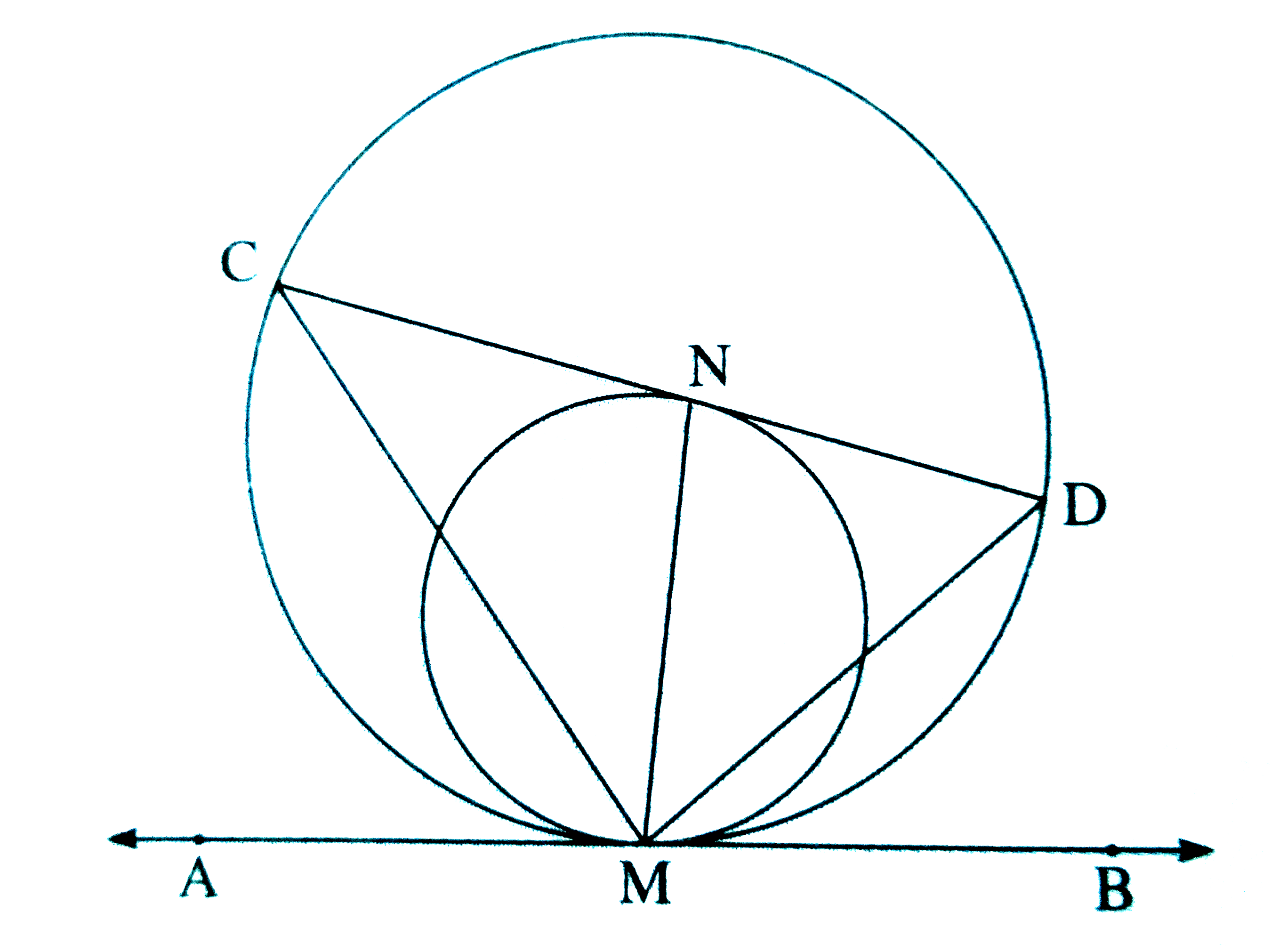
View SolutionIn the figure, M is the point of contact of two internally touching circles. The chord CD of the bigger circle touches the smaller circle at point N. Line AMB is their common tangent. Prove MN bisects ∠CMD
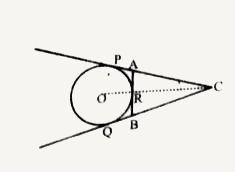
View SolutionIn figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm. Find the length of BC.
View SolutionIn figure, DE and DF are tangents from an external point D to a circle with centre A. If DE = 5 cm and DE⊥DF, then find the radius of the circle.

View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View Solution