In the figure in ΔABC, point D on side BC is such that ∠BAC=∠ADC.
Prove that CA2=CB×CD.
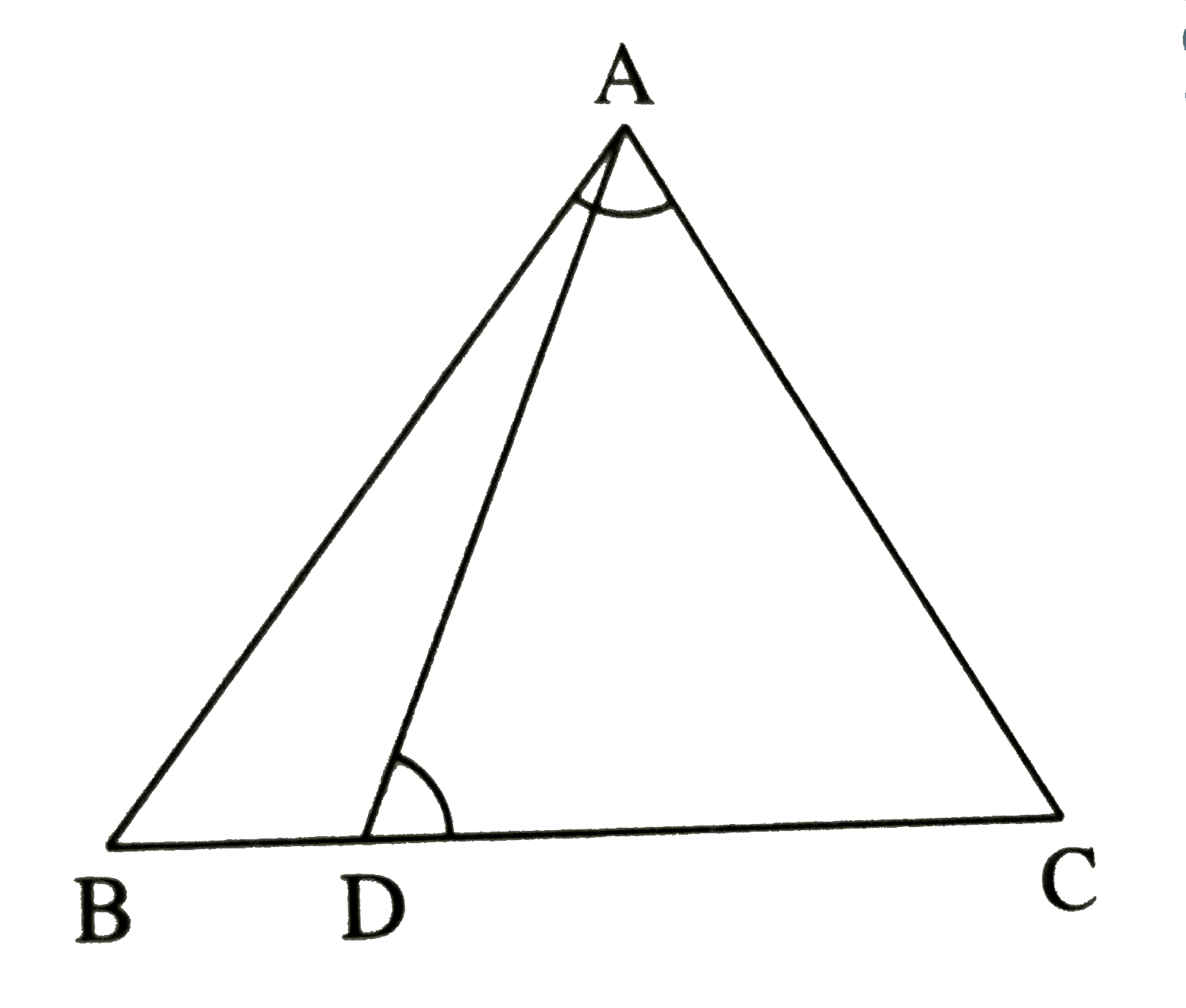
In ΔBAC and ΔADC
∠BAC≅∠ADC……(Given)
∠ACB≅∠DCA…….(Common angle)
∴ΔBAC~ΔADC…..("AA" test of similarity)
∴CACD=CBCA……(Corrresponding sides of similar triangles are proportional)
∴CA2=CB×CD.
Topper's Solved these Questions
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.5 (4 mark each)
Explore 3 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:EXAMPLE TYPE
Explore 50 Videos
- SIMILARITYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:SIMILARITYExercise:2.3 (2 mark each)
Explore 10 Videos
- QUADRATIC EQUATIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATIONS Exercise:ASSIGNEMENT 2.4
Explore 8 Videos
- STATISTICSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:STATISTICSExercise:EXAMPLES FOR PRACTICE (MCQs)
Explore 35 Videos
Similar Questions
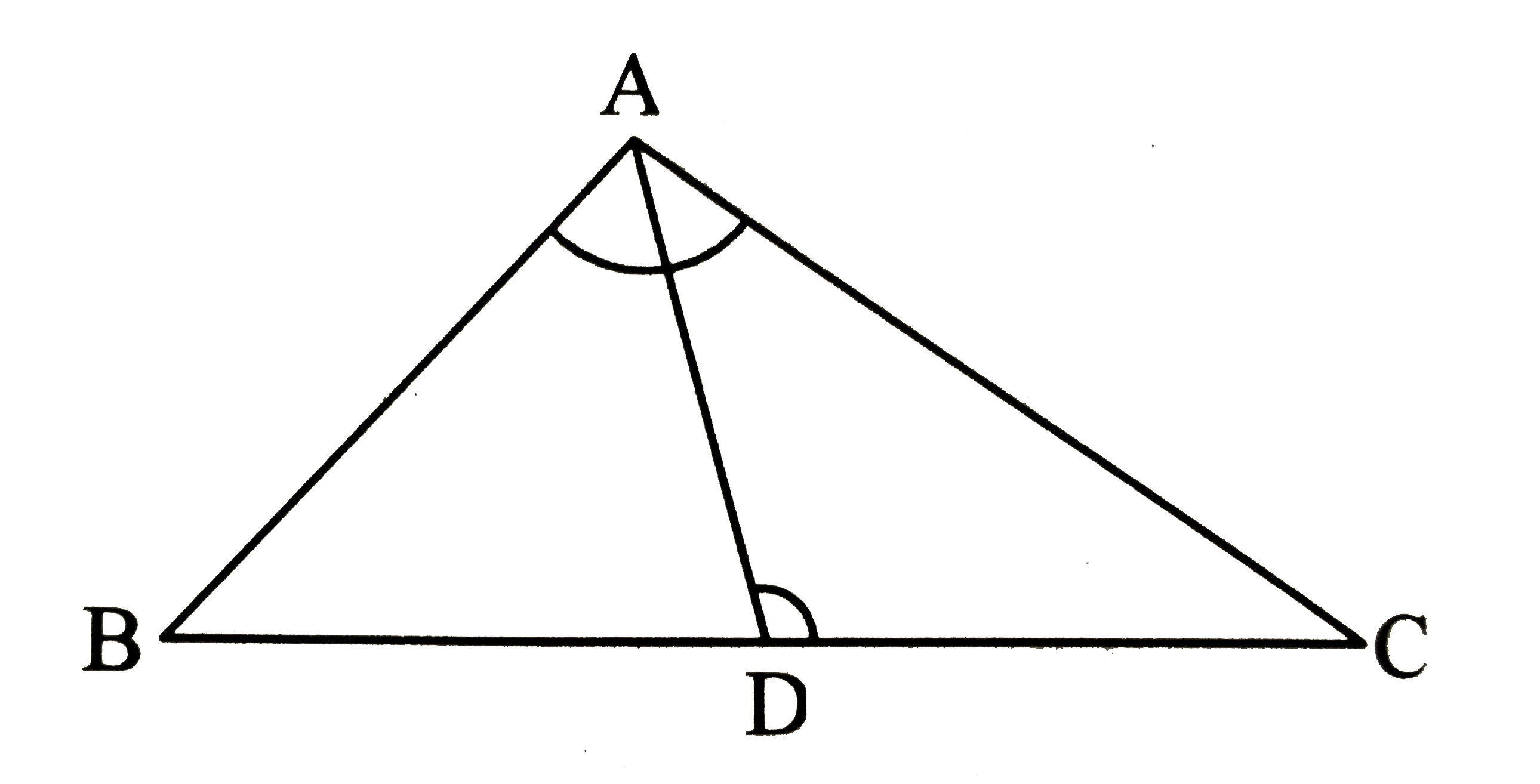
In the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
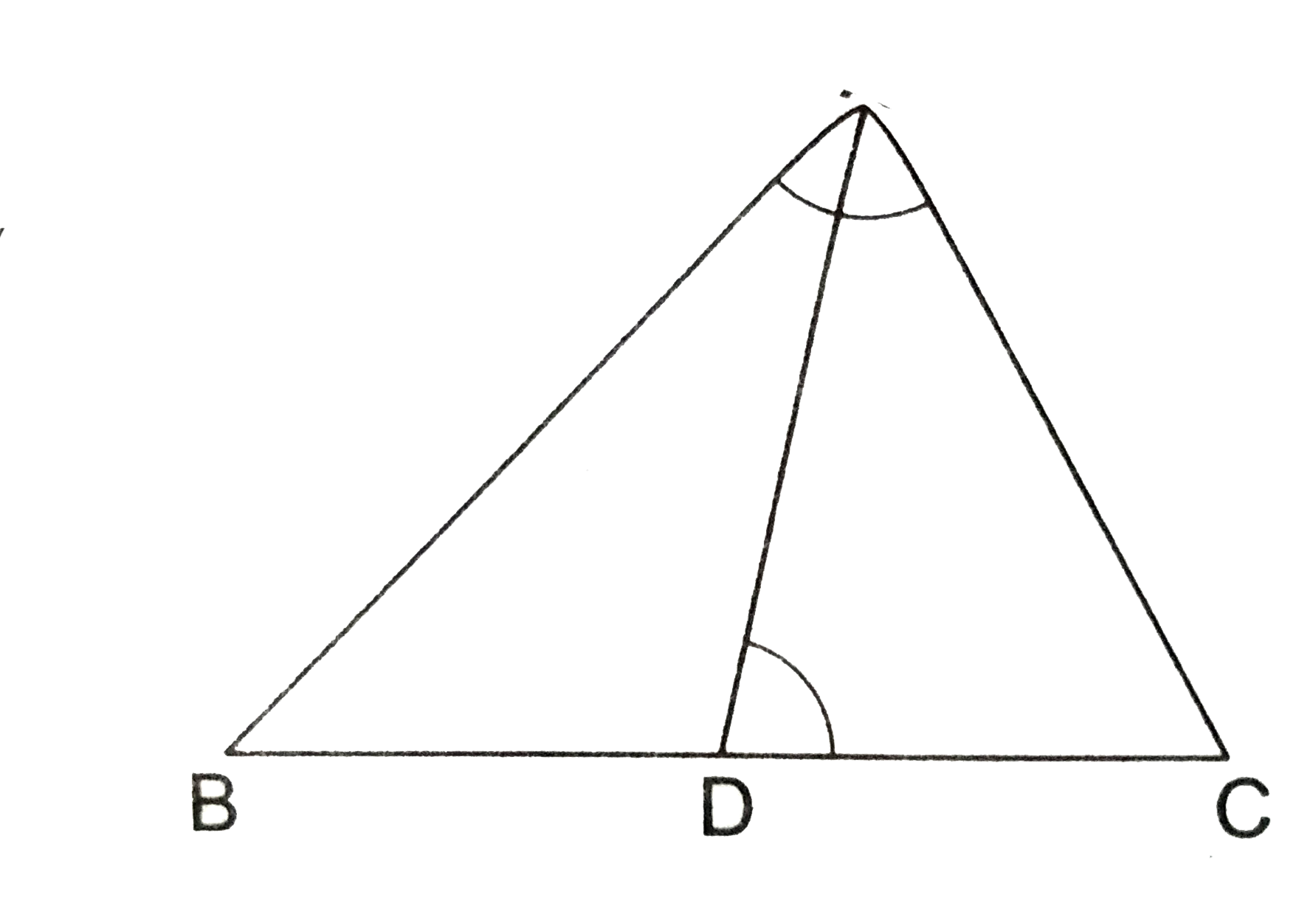
View SolutionIn the given figure , D is a point on the side BC of ΔABC such that ∠ADC=∠BAC. Prove that CA2=CB×CD.
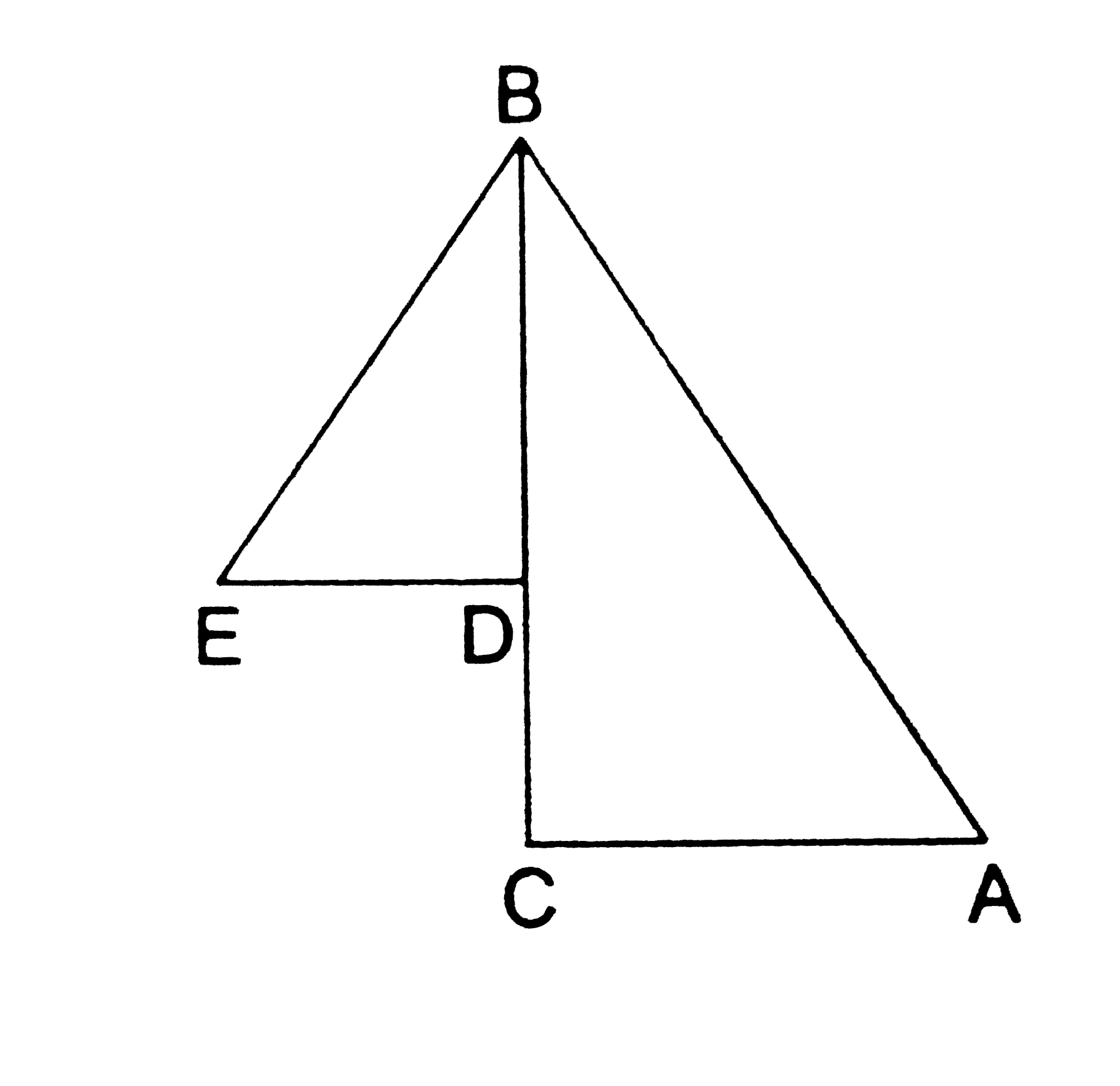
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB.CD.
View SolutionD is a point on the side BC of ABC such that ∠ADC=∠BAC . Prove that CACD=CBCA or, CA2=CB×CD .
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionIn the given figure ,P is a point on the side BC of △ABC.Prove tat (AB+BC+AC)GT2AP
View SolutionIn triangle ABC , angle B is equal to twice of angle C , D is a point on BC such that AD bisects ∠BAC and AB=AD . Prove that ∠BAC=72∘
View SolutionIn Figure, it is given that AB=CD and AD=BC. Prove that ADC ≅CBA
View Solution