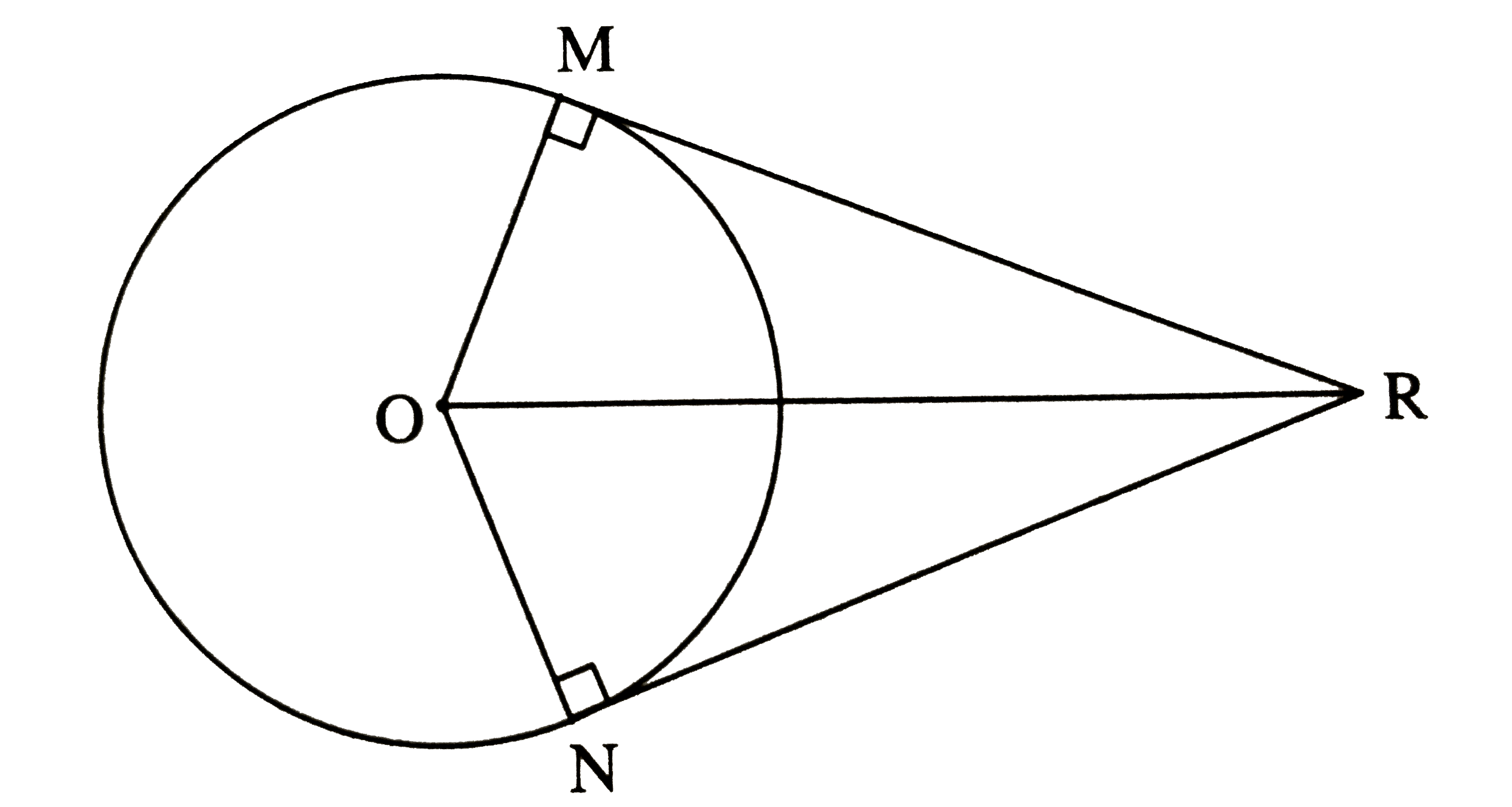
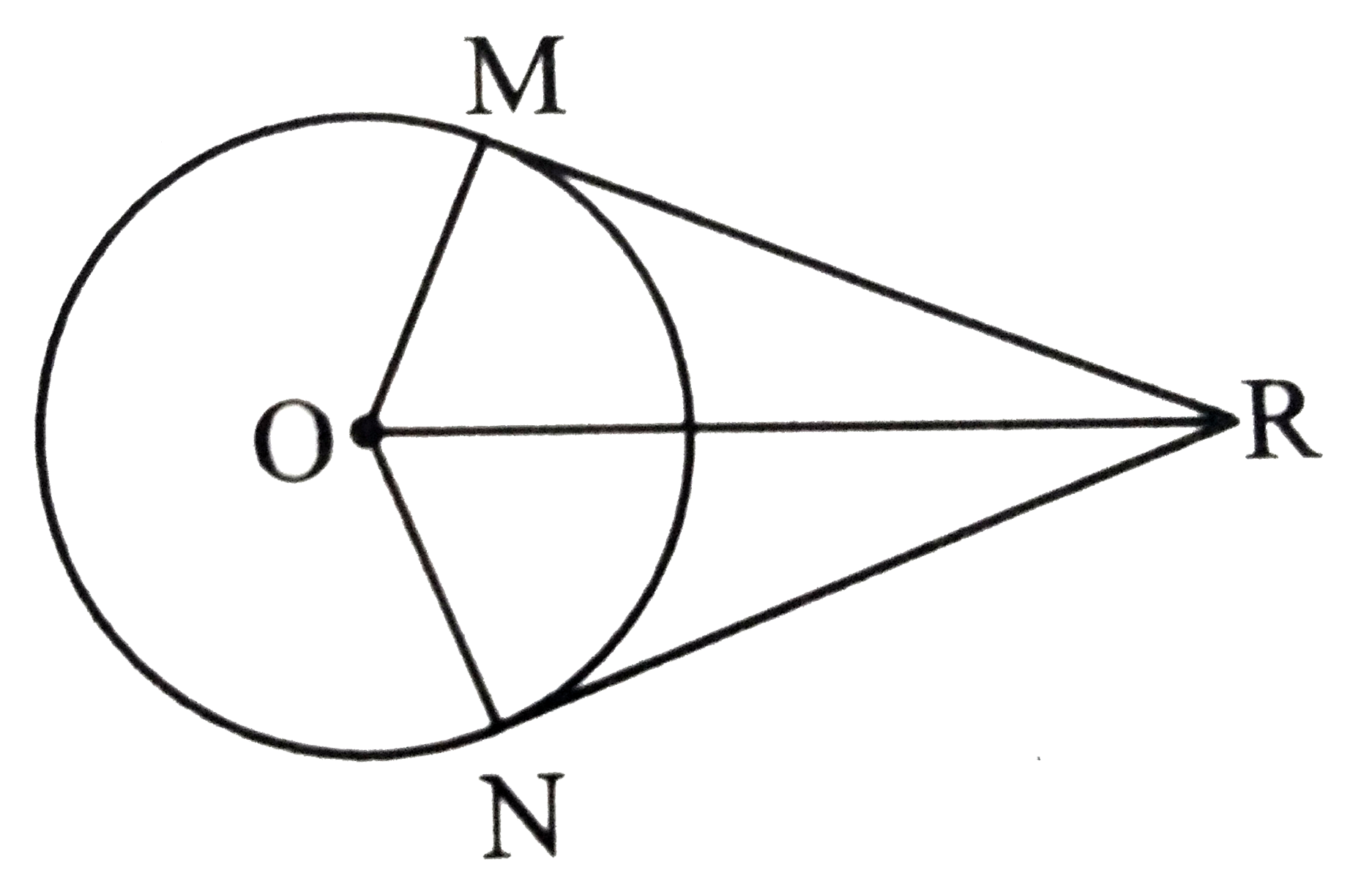
In the figure , O is the radius of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If OR = 10cm and radius of the circle = 5 cm, then (i) What is the length of each tangent segment ? (iii) What is the measure of ∠MRO ? (iii) What is the measure of ∠MRN ?
To solve the problem step-by-step, we will follow the given information and apply the relevant geometric principles.
Given:
- Length of radius OR=10 cm
- Radius of the circle OM=ON=5 cm (since M and N are points of tangency)
To Find:
1. Length of each tangent segment MR and NR
2. Measure of angle ∠MRO
3. Measure of angle ∠MRN
Step 1: Finding the Length of Each Tangent Segment
From the properties of tangents to a circle, we know that the radius at the point of tangency is perpendicular to the tangent. Therefore, in triangle OMR:
- OM is perpendicular to MR
- This makes triangle OMR a right triangle.
Using the Pythagorean theorem:
OR2=OM2+MR2
Substituting the known values:
102=52+MR2
100=25+MR2
MR2=100−25
MR2=75
MR=√75=5√3 cm
Since MR and NR are equal (both are tangent segments from point R), we have:
NR=MR=5√3 cm
Step 2: Finding the Measure of Angle ∠MRO
In triangle OMR, we can use the cosine function to find ∠MRO:
cos(∠MRO)=MROR
Substituting the values:
cos(∠MRO)=5√310=√32
Thus,
∠MRO=cos−1(√32)=30∘
Step 3: Finding the Measure of Angle ∠MRN
Since △OMR and △ONR are congruent (both have equal sides OM=ON and MR=NR), the angles ∠MRO and ∠NRO are equal:
∠NRO=∠MRO=30∘
Therefore, the angle ∠MRN is:
∠MRN=∠MRO+∠NRO=30∘+30∘=60∘
Final Answers:
1. Length of each tangent segment MR=NR=5√3 cm
2. Measure of angle ∠MRO=30∘
3. Measure of angle ∠MRN=60∘
---
- Length of radius OR=10 cm
- Radius of the circle OM=ON=5 cm (since M and N are points of tangency)
1. Length of each tangent segment MR and NR
2. Measure of angle ∠MRO
3. Measure of angle ∠MRN
- This makes triangle OMR a right triangle.
OR2=OM2+MR2
102=52+MR2
100=25+MR2
MR2=100−25
MR2=75
MR=√75=5√3 cm
NR=MR=5√3 cm
cos(∠MRO)=MROR
Substituting the values:
cos(∠MRO)=5√310=√32
Thus,
∠MRO=cos−1(√32)=30∘
∠NRO=∠MRO=30∘
∠MRN=∠MRO+∠NRO=30∘+30∘=60∘
1. Length of each tangent segment MR=NR=5√3 cm
2. Measure of angle ∠MRO=30∘
3. Measure of angle ∠MRN=60∘
Similar Questions
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then what is the length of each tangent ?
View SolutionIn the adjoining figure ,PT is tangent to a circle with centre O . if OP= 25 cm and radius of circle is 7cm , then find the length of the tangent PT .
View SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
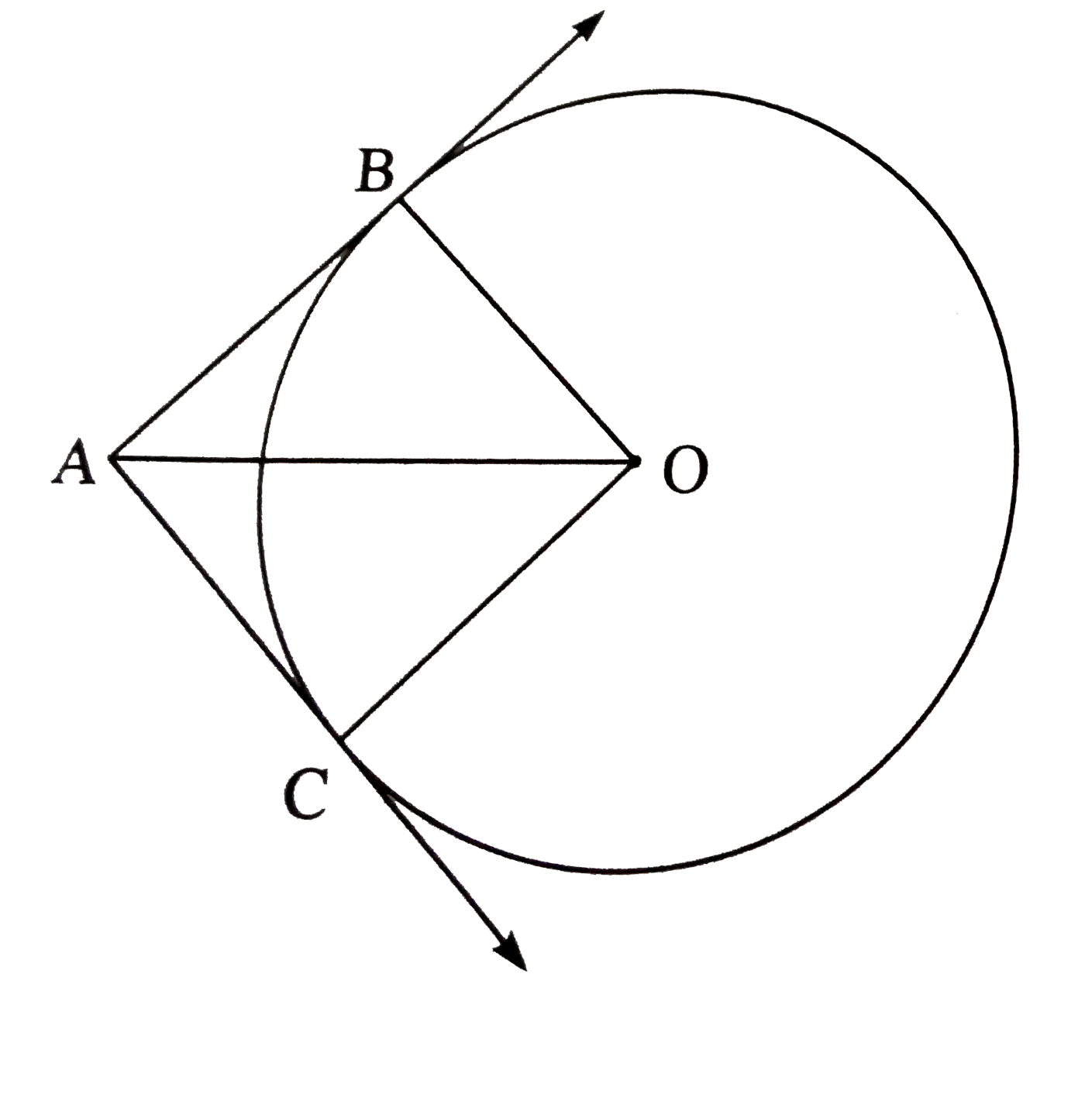
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
View SolutionIn the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
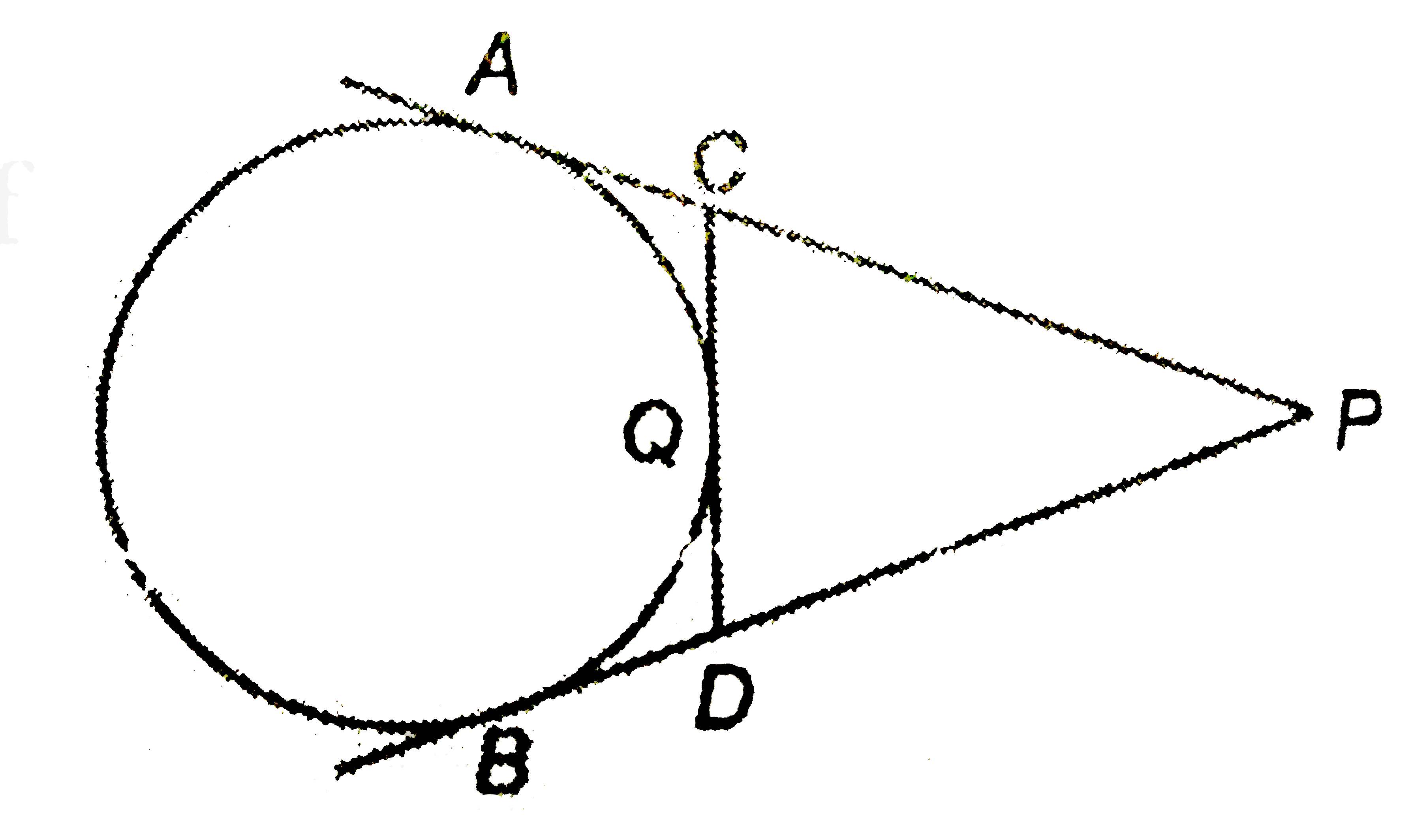
View SolutionIn the given figure, a tangent segment PA touching a circle in A and a secant PBC are shown. If AP = 15 cm and BP = 10 cm, find the length of PC.

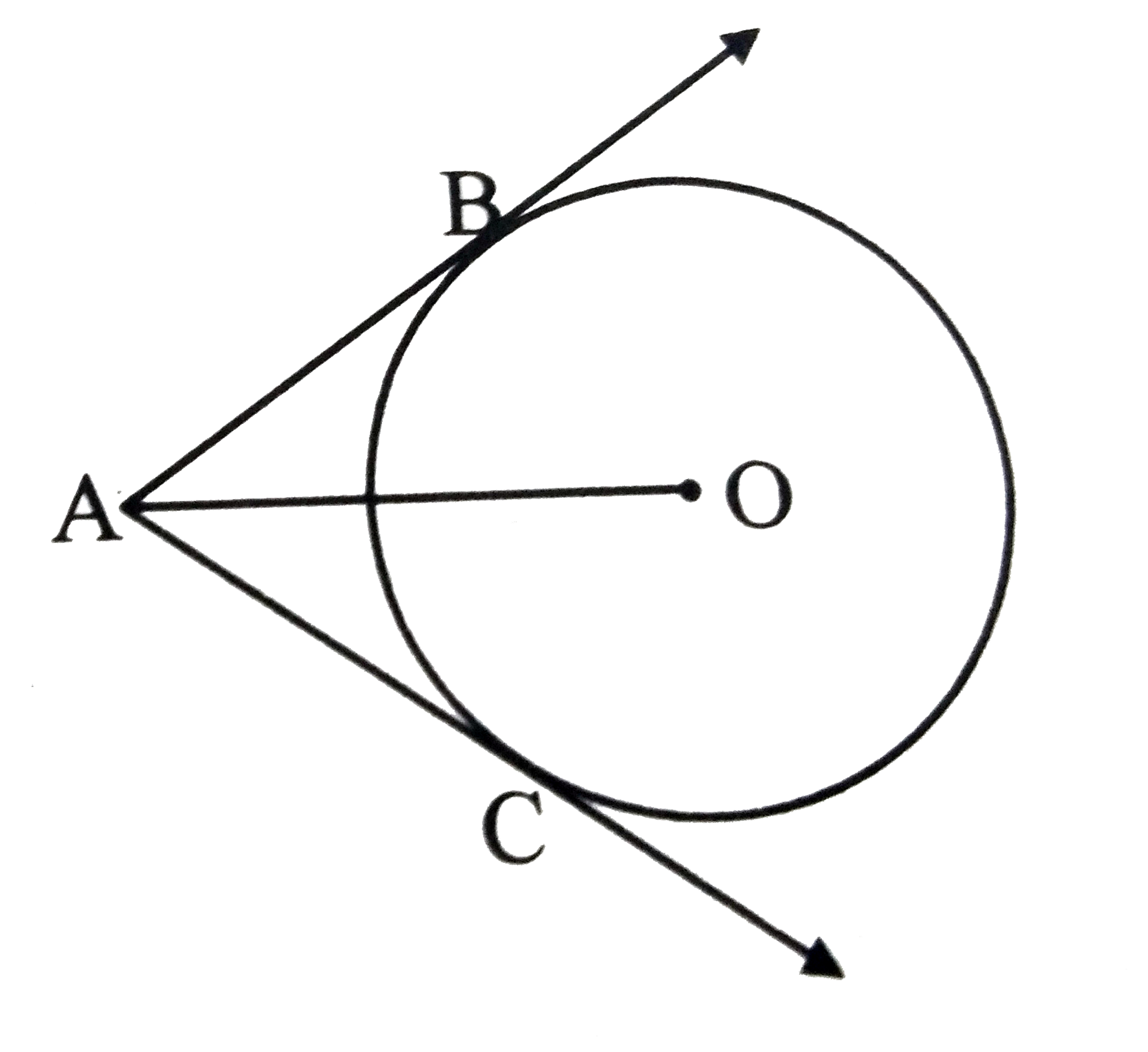
View SolutionSeg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON.
View SolutionIf the distance of point P from the centre of the circle is 13 cm and the radius of the circle is 5 cm, then length of the tangent drawn from P to the circle is :
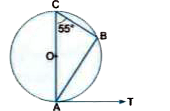
View SolutionIn Fig O is the centre of a circle and AT is a tangent at point A . what is the measure of ∠BAT ?
View SolutionSeg RM and seg RN are tangents segments of a circle with centre O. Prove that seg OR bisects∠MRN as well as ∠MON .
View Solution
