In the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
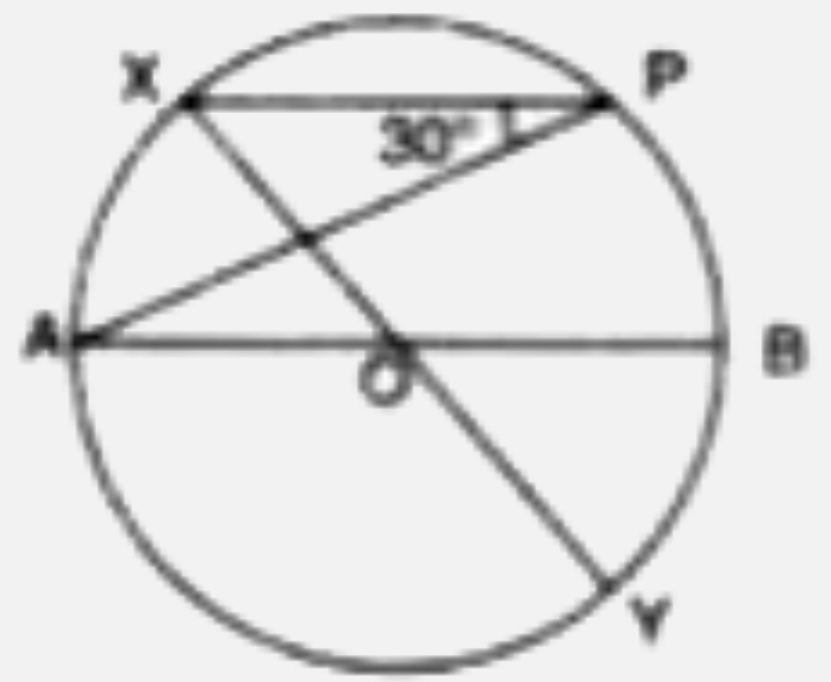
∠AOX
The correct Answer is:60∘
Step by step video solution for In the given figure, AB and XY are diameters of a circle with centre O. If angleAPX = 30^(@), find: angleAOX by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (TANGENTS AND INTERSECTING CHORDS)
Explore 10 Videos
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)
Explore 3 Videos
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (LOCI)
Explore 7 Videos
- BANKING (RECURRING DEPOSIT ACCOUNTS)Book:ICSEChapter:BANKING (RECURRING DEPOSIT ACCOUNTS)Exercise:QUESTIONS
Explore 7 Videos
- CIRCLESBook:ICSEChapter:CIRCLESExercise:EXERCISE 17( C )
Explore 28 Videos
Similar Questions
In the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
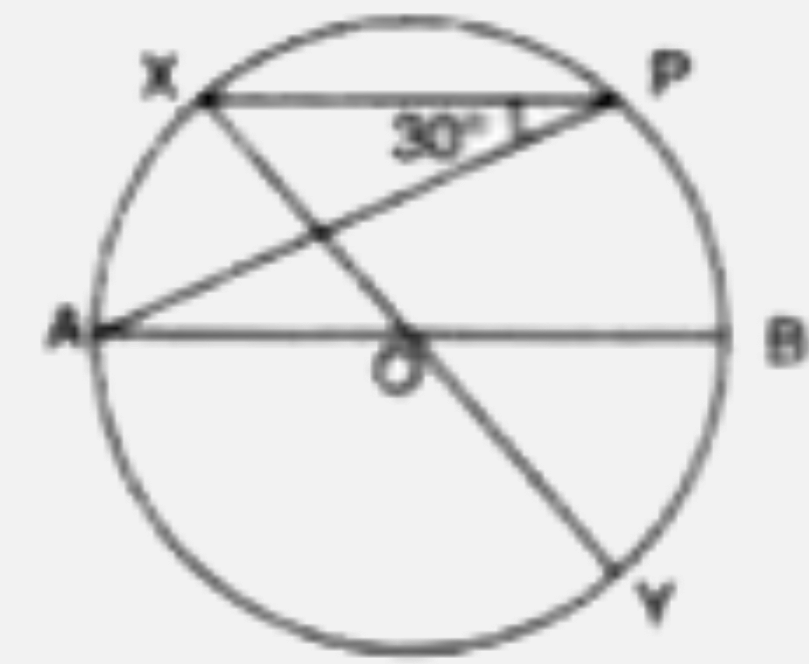
∠OAX
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠APY
View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠BPY
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
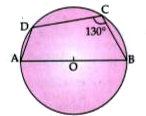
∠BCD=130∘. Find
(i) ∠DAB
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
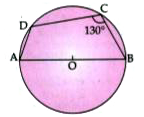
∠BCD=130∘. Find
(ii) ∠DBA
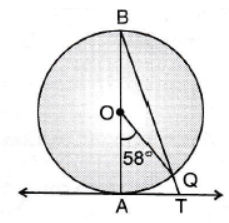
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
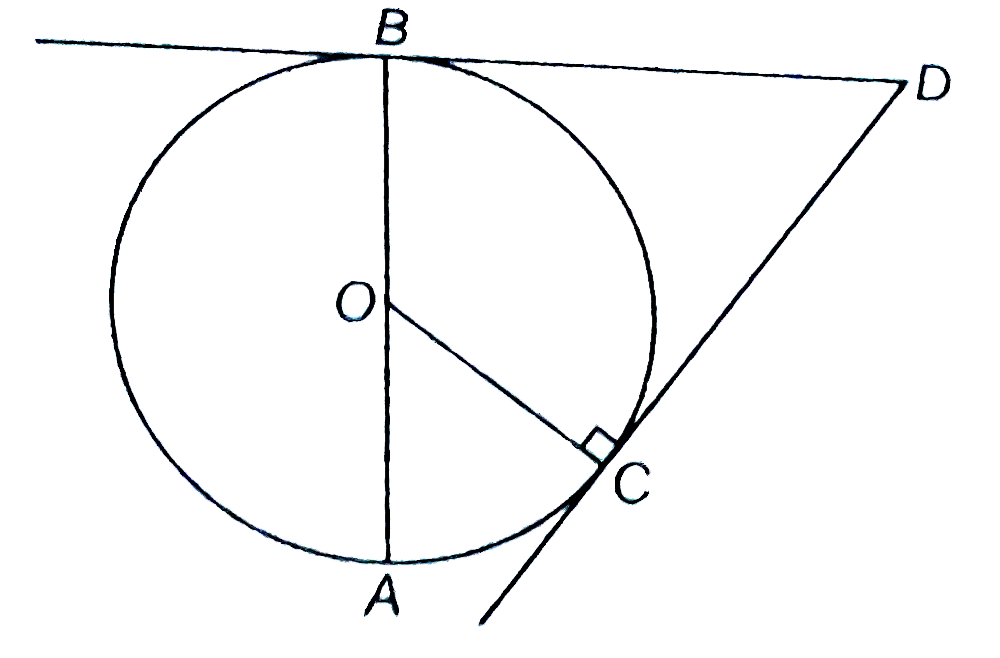
View SolutionIn the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to
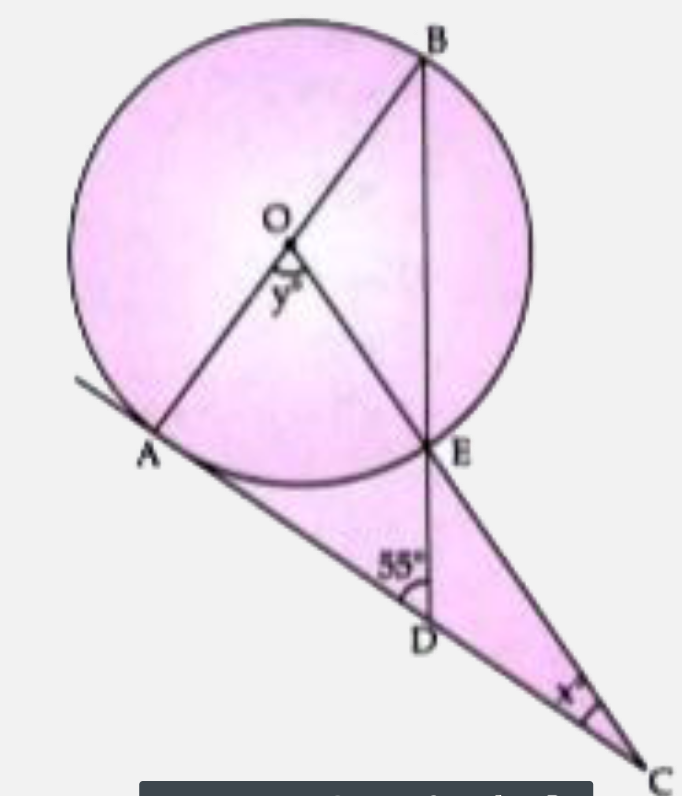
View SolutionIn the given figure AC is a tangent to the circle with centre O.
If ∠ADB=55∘, find x and y. Give reason for your answer.
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ=150∘ find angleAPQ
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View Solution