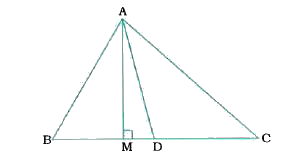
In the given figure, AD is a median of a DeltaABC and AM⊥BC. Prove that :
AC2=AD2+BC⋅DM+(BC2)2
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:AC2=AD2+BC⋅DM+(BC2)2
Step by step video, text & image solution for In the given figure, AD is a median of a DeltaABC and AM bot BC. Prove that : AC^(2)= AD^(2)+BC*DM+((BC)/(2))^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:TEST YOUR SKILLS
Explore 29 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:PRACTICE THOROUGHLY
Explore 20 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.5
Explore 23 Videos
- SURFACE AREAS AND VOLUMESBook:KUMAR PRAKASHANChapter:SURFACE AREAS AND VOLUMESExercise:TEST YOUR SKILLS
Explore 5 Videos
Similar Questions
In the given figure, DE||BC and PE||DC. If AP= 4 cm and PB= 12 cm, find AD.
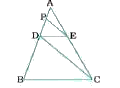
View SolutionIn ΔABC, D and E are points on the sides AB and AC respectively such that DE∣∣BC. If AB=6.75cm,AC=8.50cm and EC=6.80cm. Then find BD.
View SolutionSides of triangles are given below, Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse :
7 cm, 24 cm, 25 cm
View SolutionThe slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface at 10 per sq. m.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BE intersect at C, such that BC = CE, ∠ABC=40∘ and ∠DEC=85∘. Find ∠BAC−∠CDE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_027_Q01.png" width="80%"gt
View SolutionIn the given figure (not to scale), AC is the median as well as altitude to BD. In △ACE, AD is the median to CE. Which of the following is true?
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_010_Q01.png" width="80%"gt
View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E05_005_Q01.png" width="80%"gt
View Solution