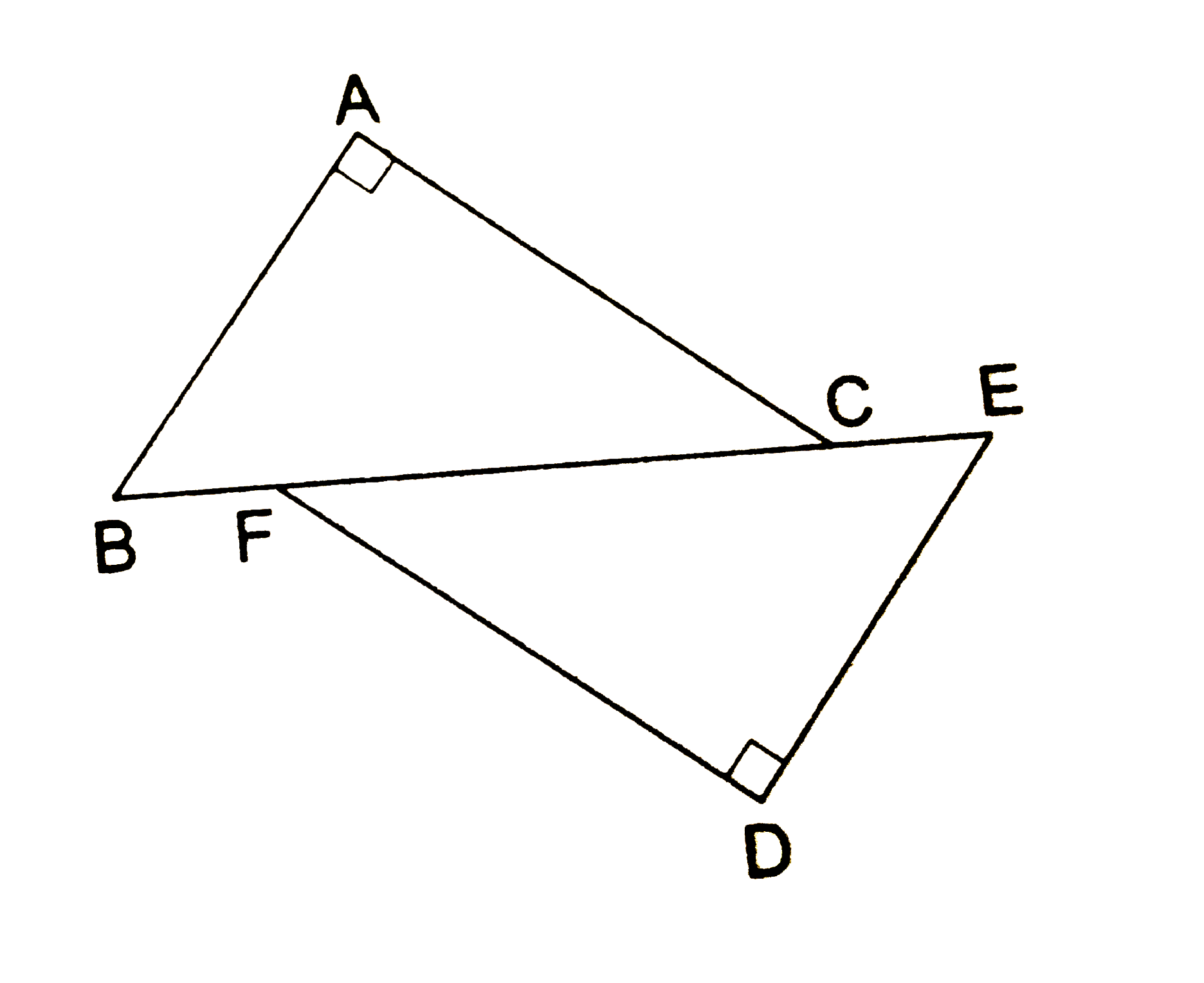
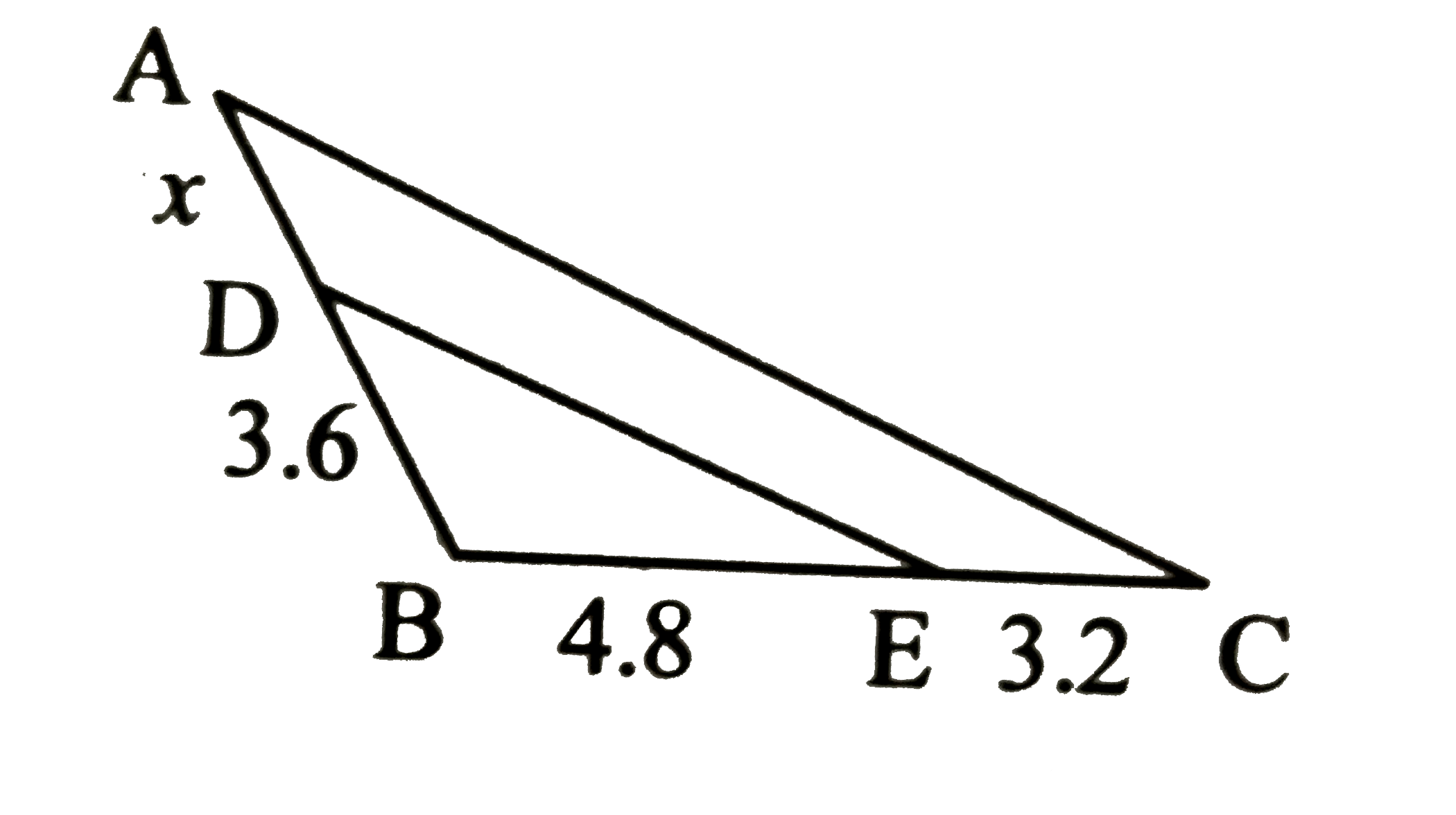In the given figure, BE and CF are two equal altitudes of ΔABC.
Show that (i) ΔABE≅ΔACF,
(ii)AB = AC.

ΔABE≅ΔACFasBE=CF,∠BAE=∠CAF=∠A,∠AEB=∠AFC=90∘
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
In given figure, FE = AC, ΔABC≅ ____.
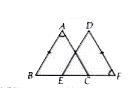 AΔDEFBΔFDECΔDFEDΔFED
AΔDEFBΔFDECΔDFEDΔFED
In the figure ,if ΔABE≅ΔACD , Show that ΔADE~ΔABC .
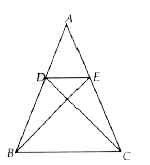
View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.

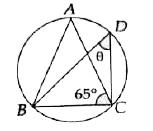
View SolutionIn the given figure if AB=AC then find θ.
View SolutionIn the given figure, BA⊥ACandDE⊥DF such that AB = DE and BF = EC. Show that ΔABC≅ΔDEF.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
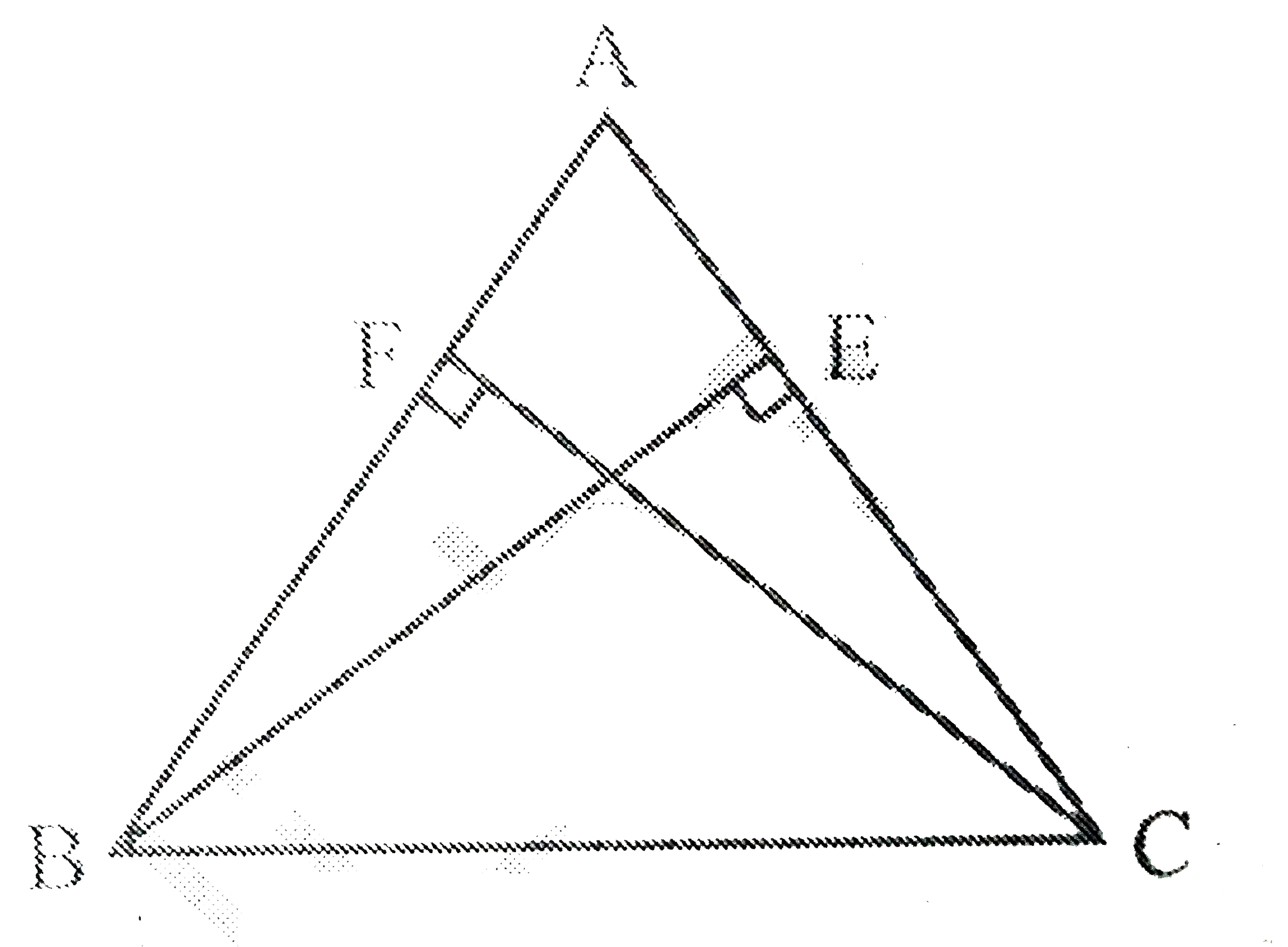
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
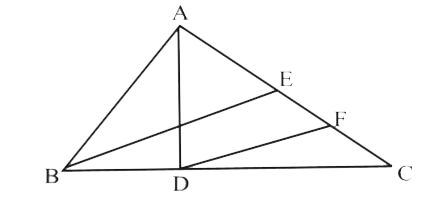
View SolutionIn the given figure AD and BE are the medians of ΔABC and BE || DF . Prove that CF=1/4AC.
View Solution