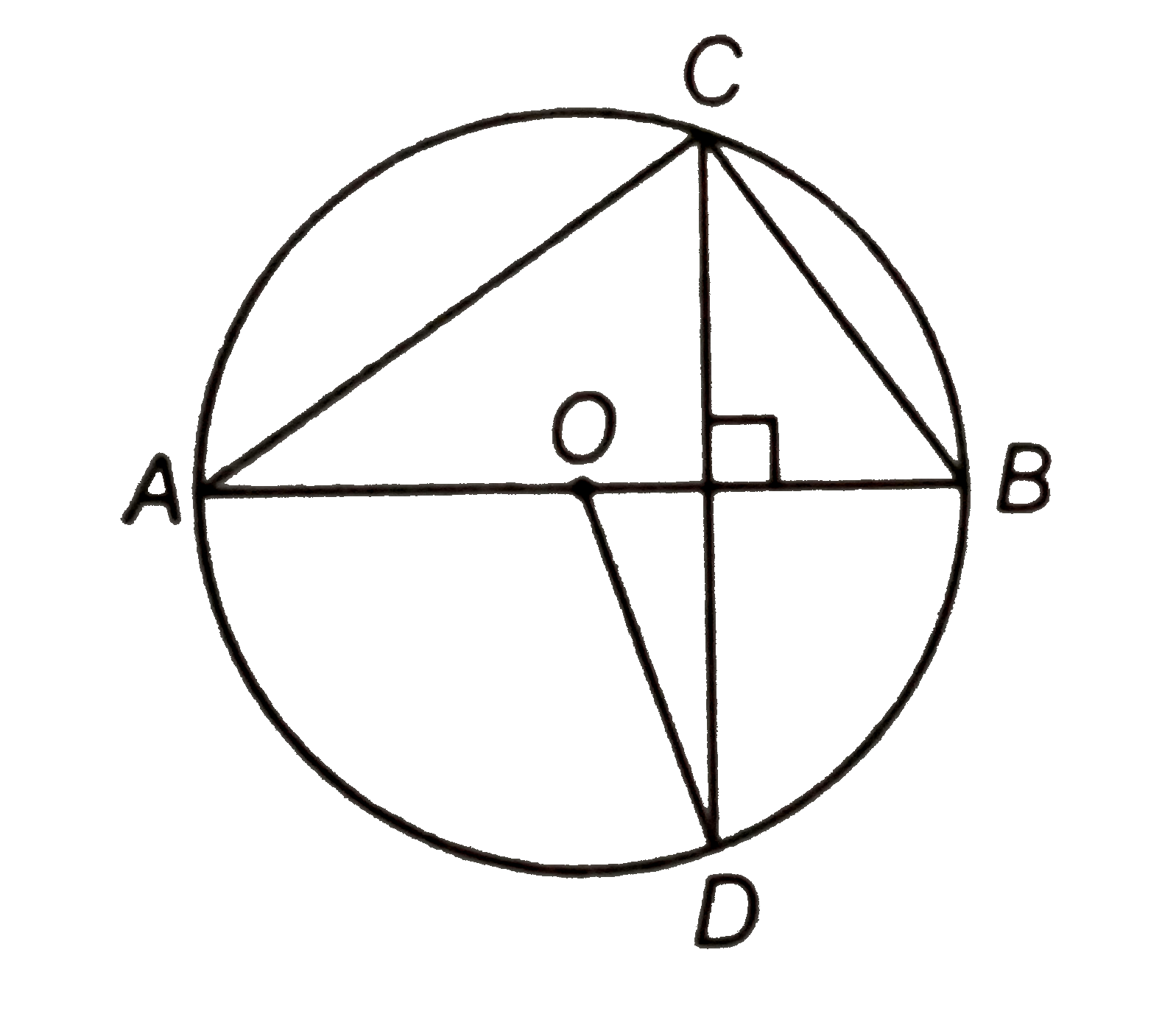
In the given figure, O is the centre of the circle, BD=OD and CD⊥AB. Find ∠CAB.
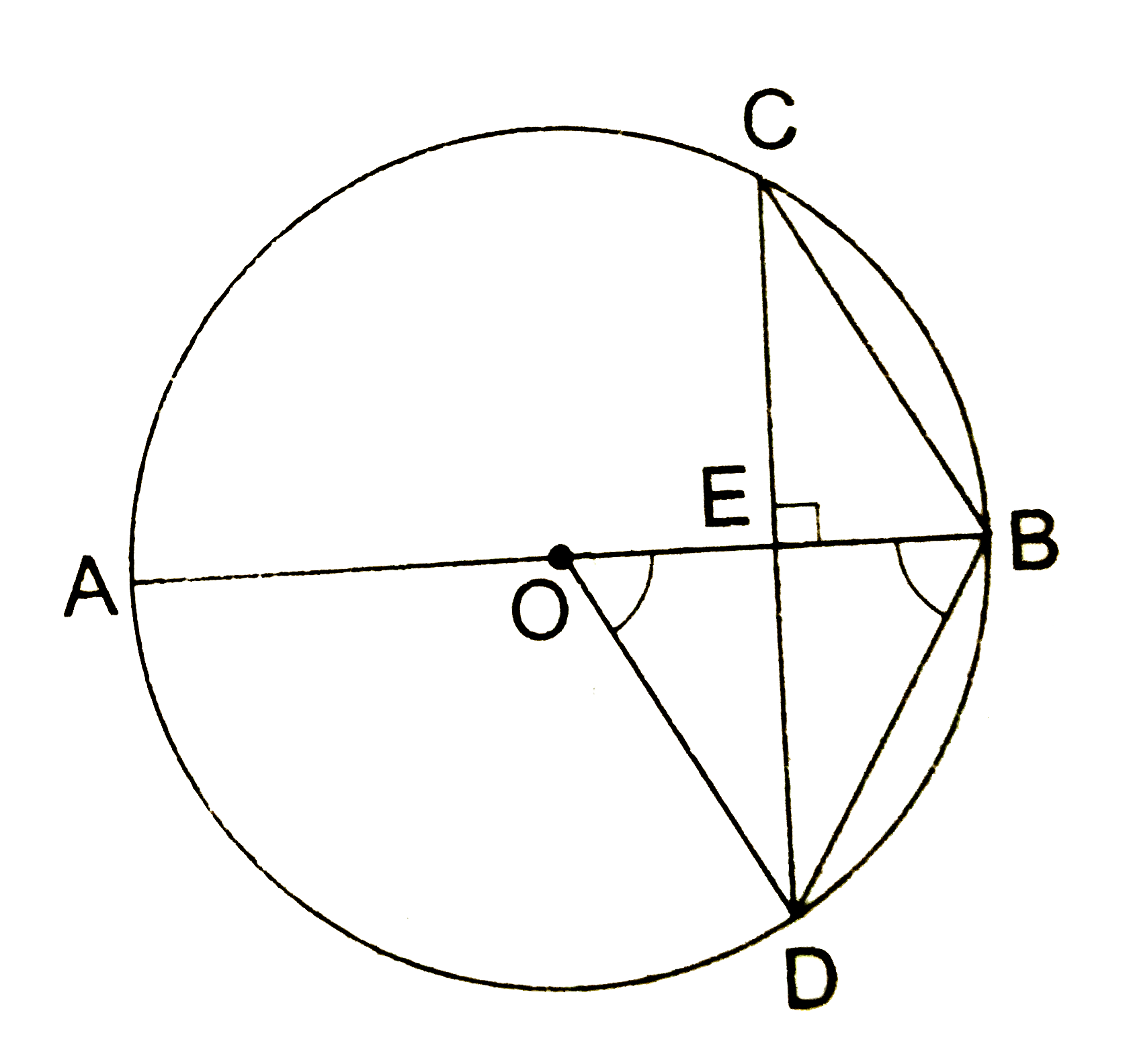
The correct Answer is:∠CAB=30∘
BD=ODand OD=OB ( radii of a circle. )
⇒BD=OD=OB
⇒ΔBDO is equilateral ⇒∠BDO=60∘
Since the altitude of an equilateral triangle bisects the vertical angle, so ∠BDE=∠ODE=30∘
∴∠CAB=∠BDE=30∘ ( angles in the same segment ).
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. Given that OD = OE = 3 cm and AD = 4 cm. Find the length of the longest chord.
 A6 cmB8 cmC10 cmD9 cm
A6 cmB8 cmC10 cmD9 cmIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
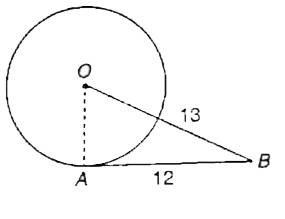 A6.5 cmB6 cmC5 cmDnone of these
A6.5 cmB6 cmC5 cmDnone of these
In the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View Solution
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
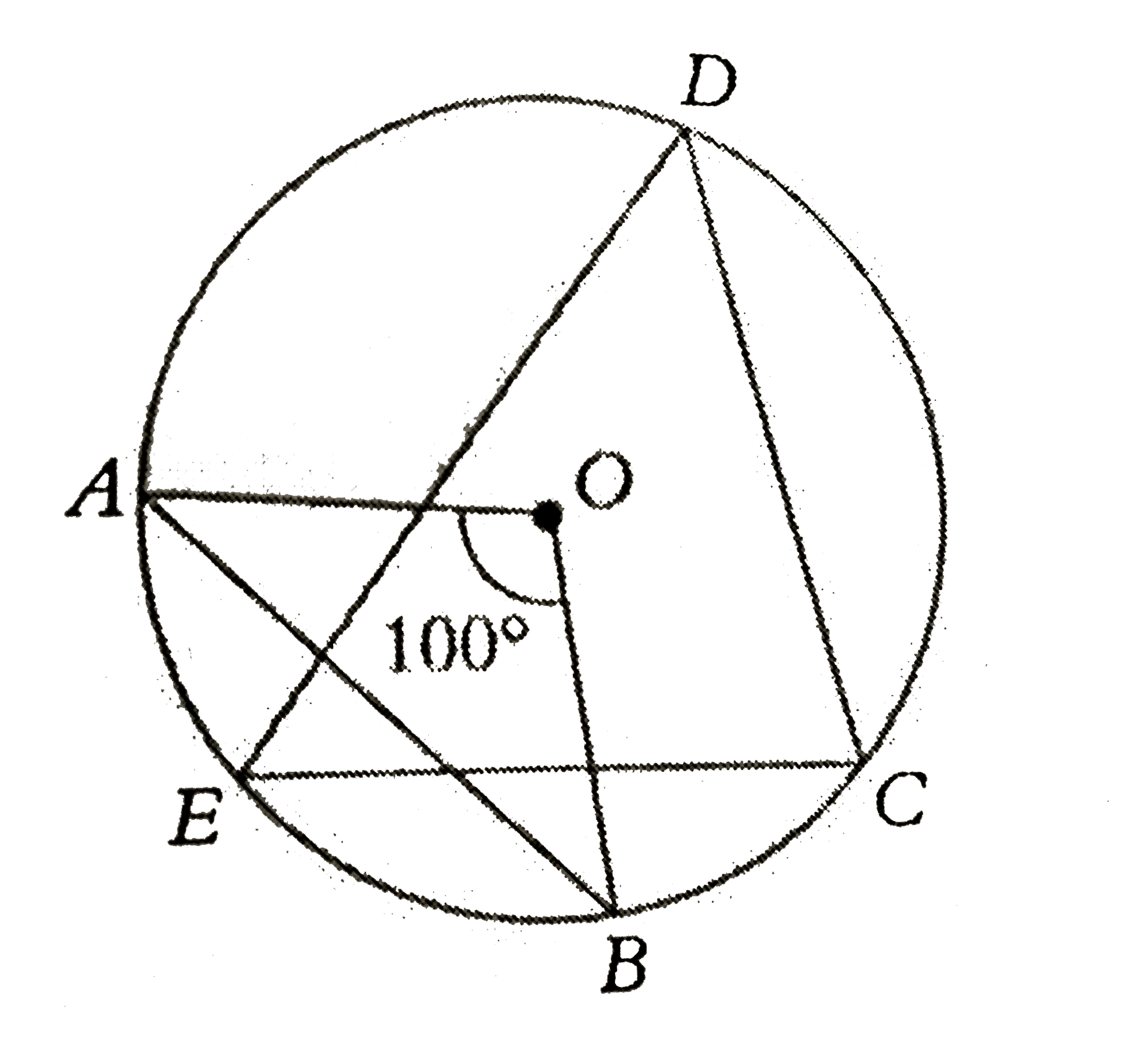
View Solution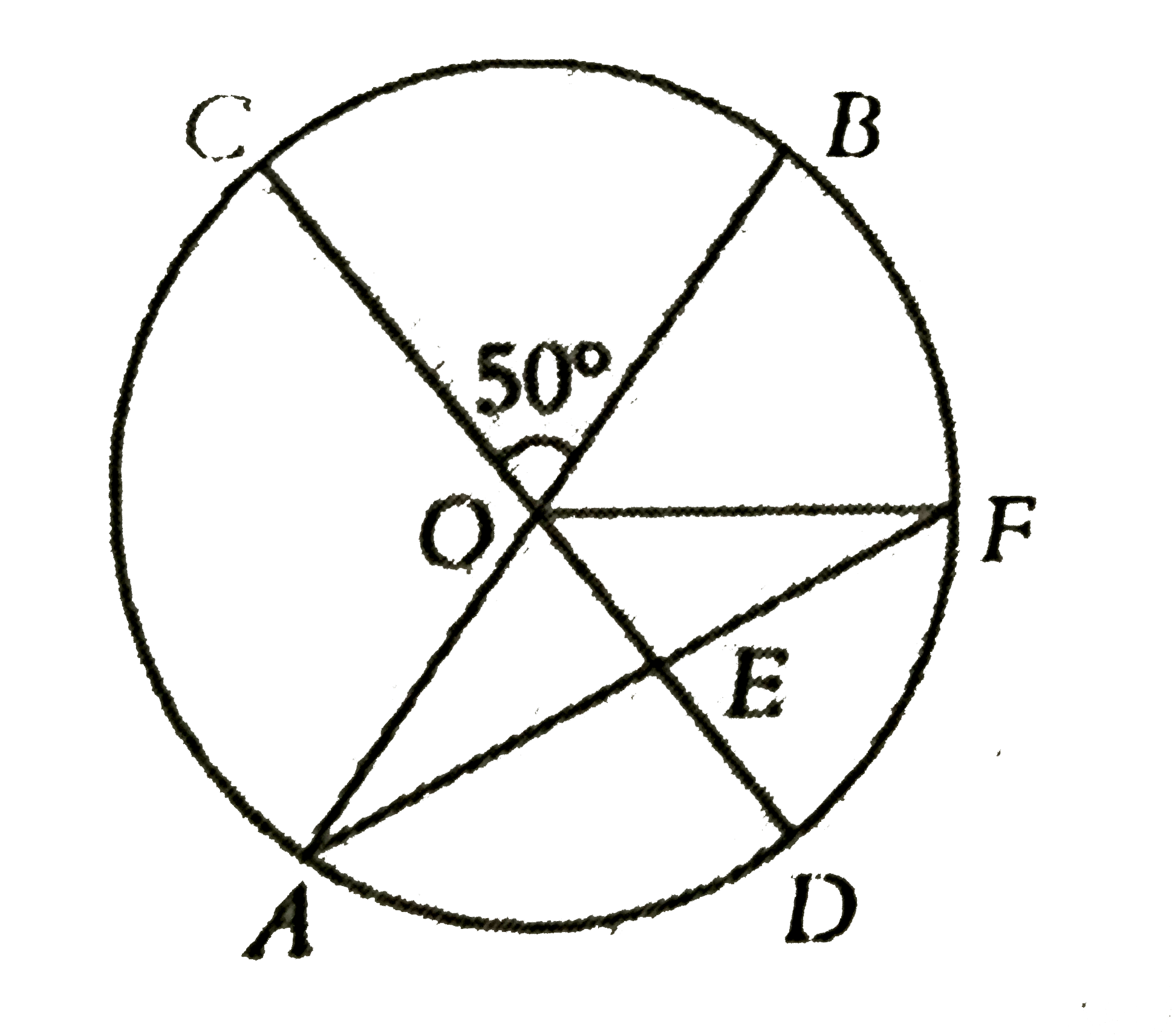
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADF
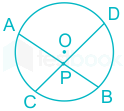
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
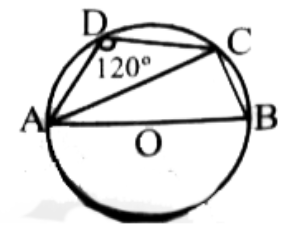
View SolutionIn the given figure, AB is the diameter of the circle. ∠ADC=120∘. Find ∠CAB :
View Solution