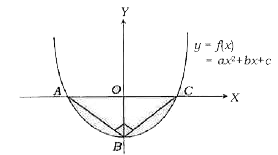
In the given figure, vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units. Number of integral values of k for which one root of f(x)=0 is more than k and other less than kSolution in Tamil
6
4
5
7
The correct Answer is:3
f(x)=0
⇒x2/(2√2)−2√2=0 or x=±2√2
Therefore, number of integral values of K for which for which k lies in (−2√2,2√2) is 5.
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise (Matrix)
Explore 3 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise (Numerical)
Explore 25 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:Exercise (Multiple)
Explore 19 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:JEE Advanced Previous Year
Explore 4 Videos
- THREE DIMENSIONAL GEOMETRYBook:CENGAGEChapter:THREE DIMENSIONAL GEOMETRYExercise:Question Bank
Explore 12 Videos
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionIf x=2+223+213, then the value of x3−6x2+6x is:
View SolutionIf one root of the quadratic equation px2+qx+r=0(p≠0) is a surd √a√a+√a−b, where p,q,r;a,b are all rationals then the other root is -
View Solutionabout to only mathematics
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionIn the given figure,vertices of Delta ABC lie on y=f(x)=ax^(2)+bx+c. The Delta ABC is right angled isosceles triangle whose hypotenuse AC=4sqrt(2) units.Number of integral values of k sqrt(2) which one root of f(x)=0 is more than k and other less than k
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
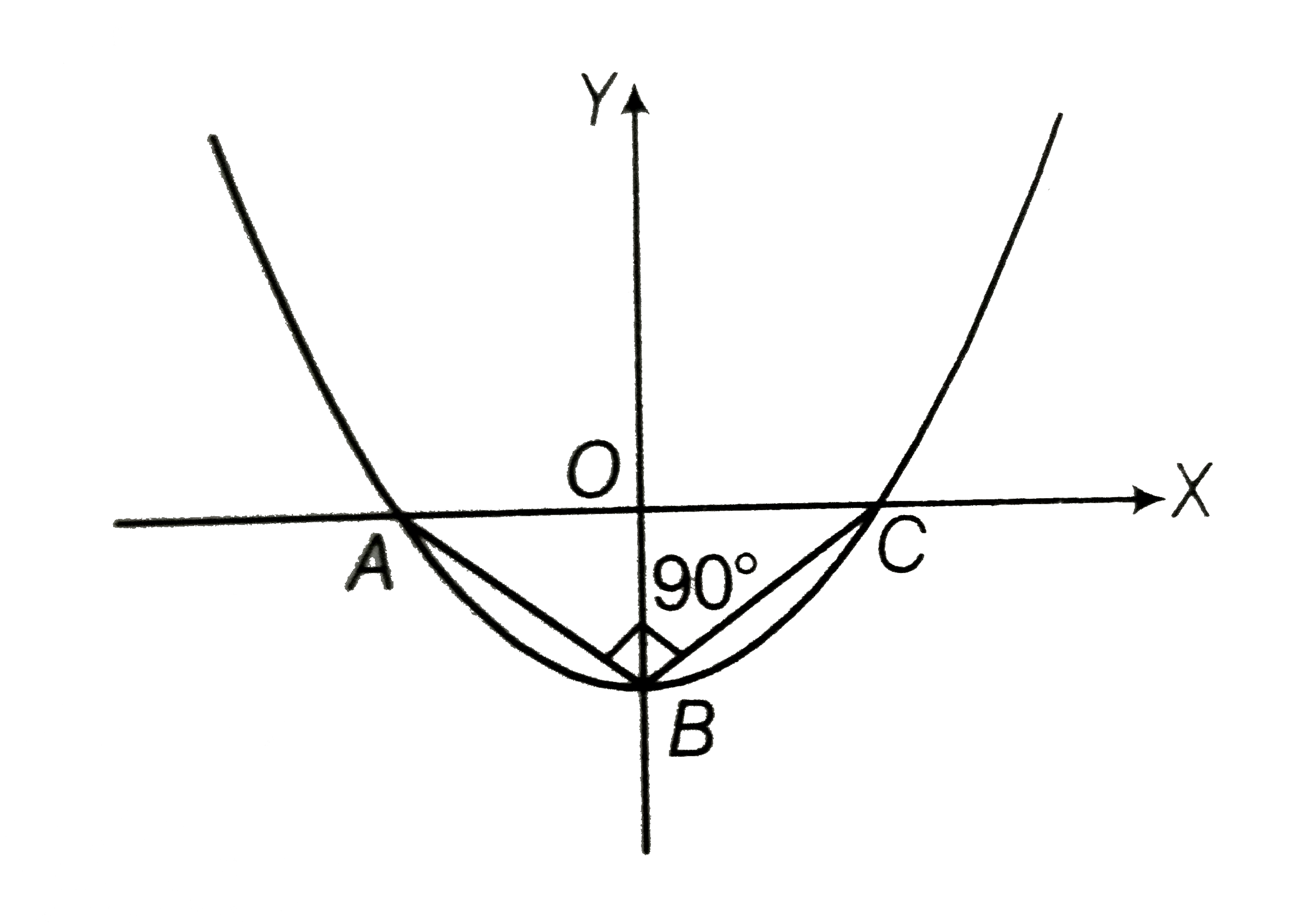
y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
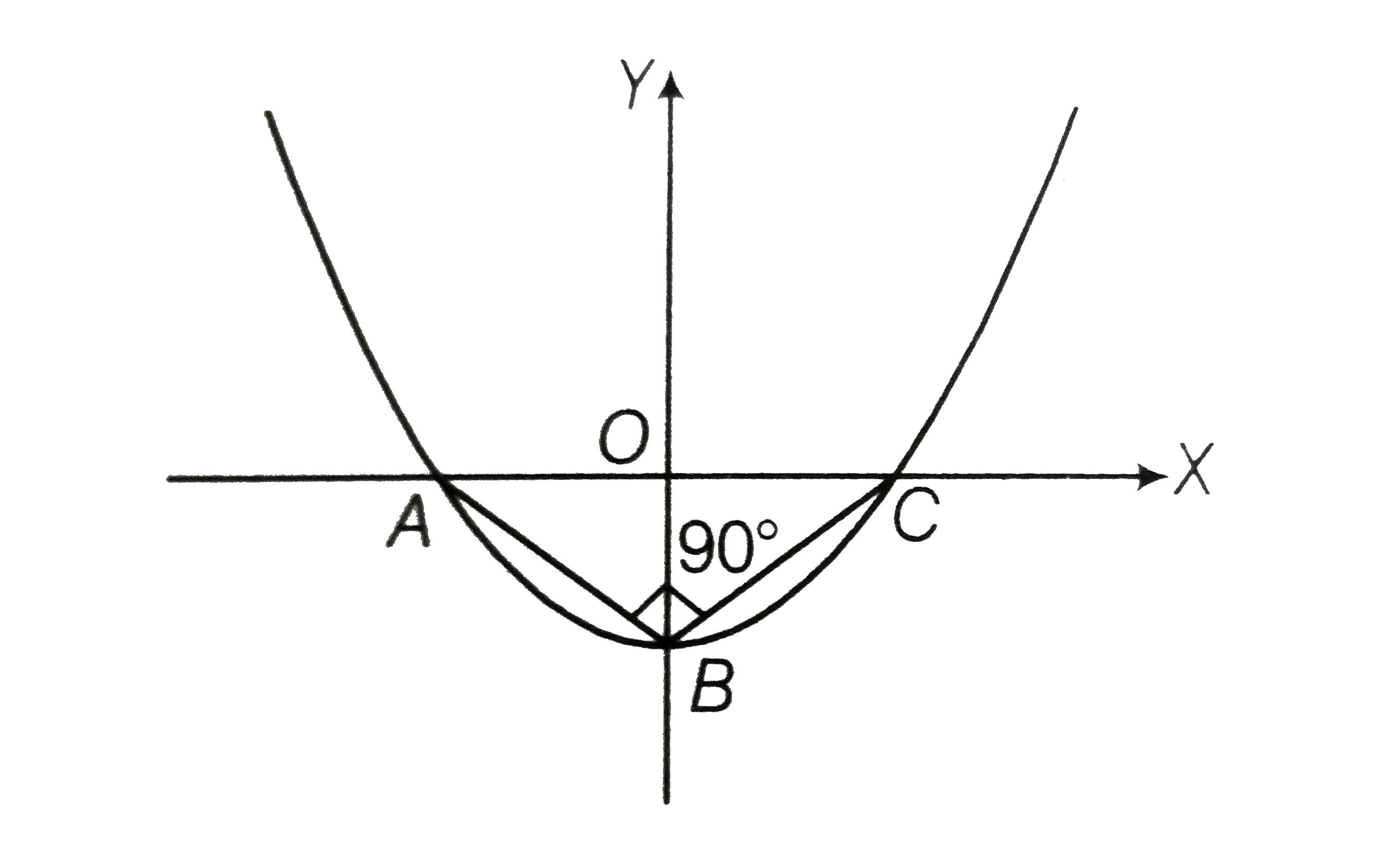
Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
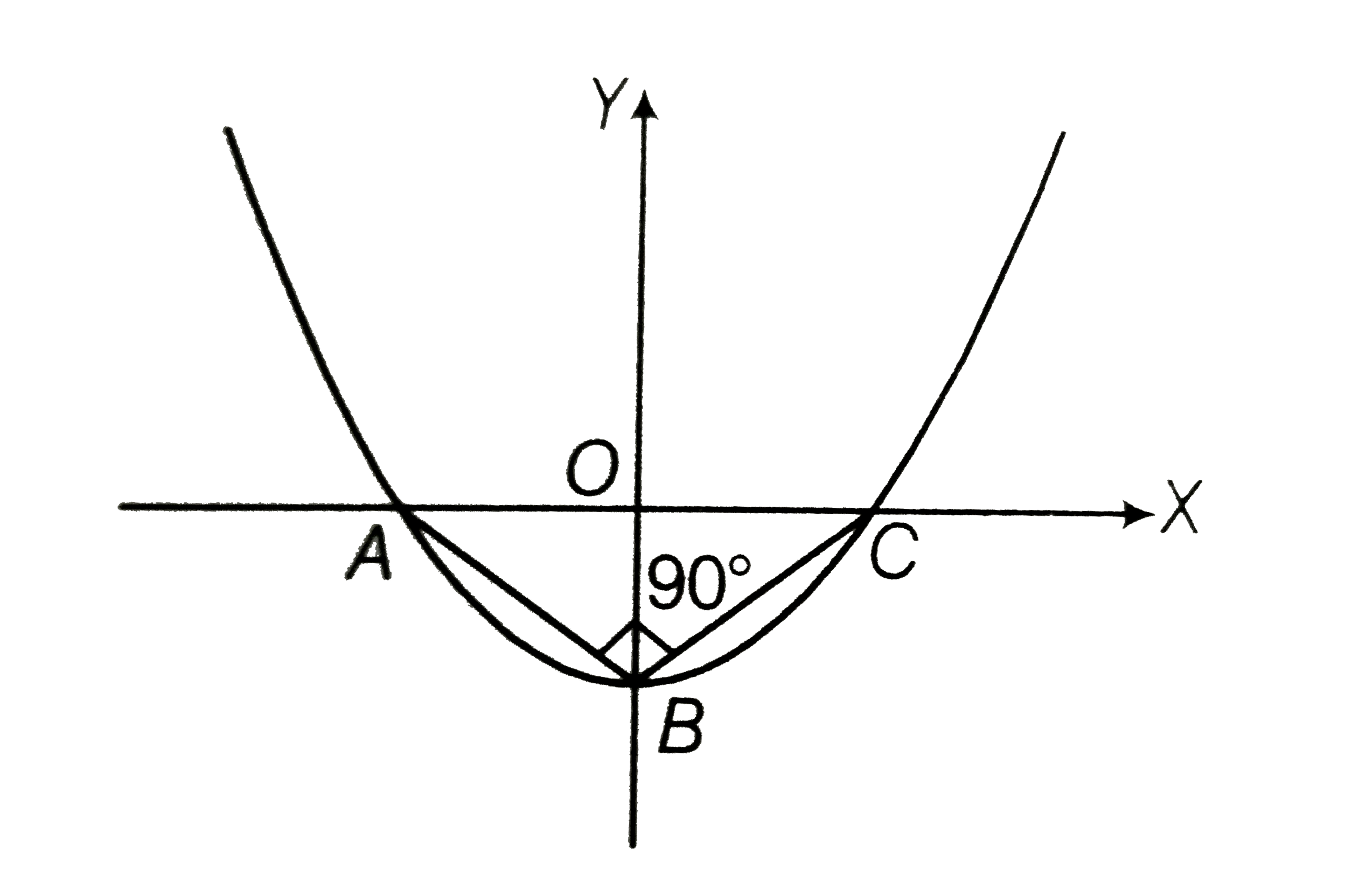
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब

y=f(x) दिया गया है
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब
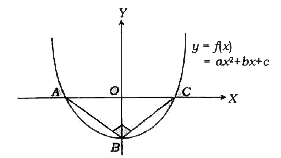
समीकरण y=f(x) का न्यूनतम मान है
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब
k के पूर्णांक मानों की संख्या जिसके लिए k2,f(x)=0 के मूलों के बीच स्थित है
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View Solution
