In triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then Solution in Tamil
locus of P is an ellipse with eccentricity √23
locus of P is a hyperbola with eccentricity √32
area of the quadr5ilateral ABCD=163 sq. units
area of the quadrilateral ABCD=323 sq. units
The correct Answer is:A, C
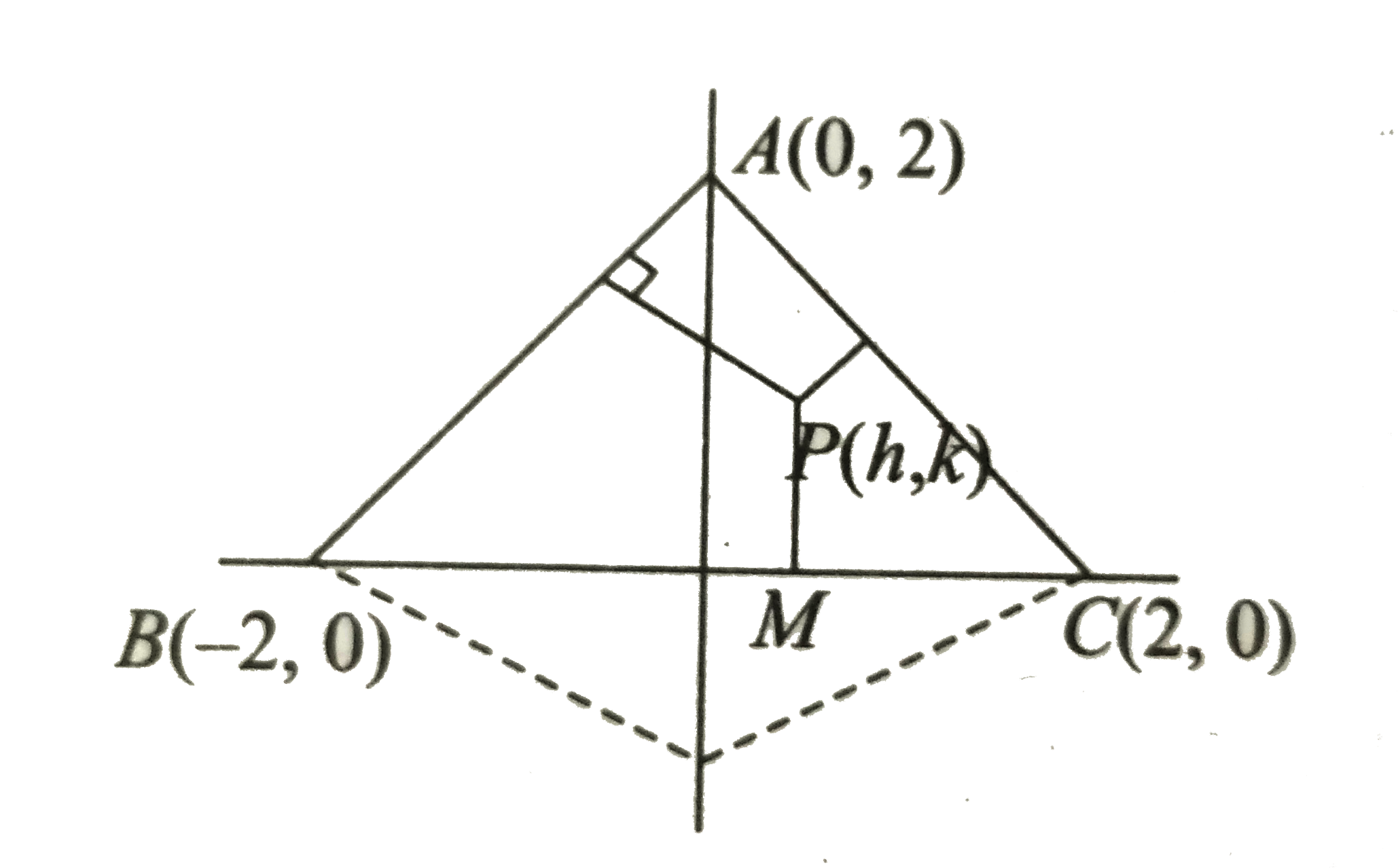
PM=k
Equation of AB≡x+y=2
Equation of AC≡x+y=2
According to question
(2−h−k√2)(2+h+k√2)=2k2
⇒h2+3k2+4k=4
⇒h2+3(k2+43k+49)=4+43
⇒h2+3(k+23)2=163⇒h216/3+(k+23)216/9=1
⇒ Ellipse with e=√23 and D≡(0,−23).
Topper's Solved these Questions
Similar Questions
Let a,b>0 and →α=(→ia+4ˆjb+bˆk) and →β=bˆi+aˆj+1bˆk, then the maximum value of 305+→α.→β is
View SolutionLet any double ordinate PNP' of the hyperbola x225−y216=1 be produced on both sides to meet the asymptotes in QandQ' . Then PQ.P′Q is equal to 25 (b) 16 (c) 41 (d) none of these
View SolutionABCD is a square with side AB=2. A point P moves such that its distance from A equals its distance from the line BD.The locus of P meets the line AC at T_(1) and the line through A parallel to BD at T_(2) and T_(3). The area of the triangle T_(1)T_(2)T_(3) is :
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionABC is an isosceles triangle with its base BC twice its altitude.A polnt P moves within the triangle such that the square of its distance from BC is half the rectangle contained by its distances from the two sides.Show that the locus of P is an ellipse with eccentricity sqrt((2)/(3)) passing through B&C.
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length a of a rectangle is twice the sum of the squares of its distances from the other two sides of length b.The locus of the point can be:
View SolutionIn triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0)andB(−a,0) is constant and equal to 6a2. The locus of P is
View SolutionIf A(−2,1),B(0,−2),C(1,2) are the vertices of a triangle ABC, then the perpendicular distance from its circumcentre to the side BC is
View SolutionIf A(-2,1), B(0,-2), C(1,2) are the vertices of a triangle ABC , then the perpendicular distance from its circumference of the side BC is ,
View SolutionThere is a point inside an equilateral triangle ABC of side d whose distance from the vertices is 3,4,5 . Rotate the triangle and P through 60∘ about C. Let A go to A' and P to P'.
The value of d2 is
View SolutionStatement 1: In a triangle ABC , If base BC is fixed and perimeter of the triangle is constant, then vertex A moves on an Ellipse.
Statement 2: If the sum of distances of a point P from two fixed points
is constant then locus of P is a real ellipse
View SolutionIn triangle ABC,a=4 and b=c=2√2. A point P moves within the triangle such that the square of its distance from BC is half the area of rectangle contained by its distance from the other two sides. If D be the centre of locus of P, then
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0),B(−a,0) is 8a2 the locus of P is
View Solution
