inside the circles x2+y2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to
√2(√2−1)
√3(2−√3)
√2(2−√3)
√3(√3−1)
The correct Answer is:B

We have AC=2a
and OA=OC=1−a (since circles are touching internally)
Since ΔABCis equilateral, we have
∴∠AOC=120∘
Using cosine rule, we have
cos120∘=(1−a)2+(1−a)2−(2a)22(1−a)(1−a)
⇒−12=−a2−2a+1(1−a)2
⇒a2−2a+1=2a2+4a−2
⇒a2+6a−3=0
⇒a=−6+√482=√3(2−√3)
Similar Questions
बराबर त्रिज्या r तथा केडेरो (0,0), (1,1) तथा (2, 1) वाले तीन वृत चित्रानुसार दिखाए गए है। यदि उनकीउभयनिष्ठ स्पर्श रेखा चित्रानुसार है तो 'r' का मान होगा
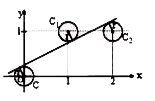
View Solutionइकाई त्रिज्या के तीन समान वृत्त एक दूसरे को स्पर्श करते है। तीनों वृत्तों को स्पर्श करने वृत्त की त्रिज्या है -
View SolutionThree equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
View SolutionLocus of the poirit of intersection of the pair of perpendicular tangents to the circles x2+y2=1 and x2+ y2=7 is the director circle of the circle with radius equal to
View Solutionतीन समान वृत्त जिनमें प्रत्येक की त्रिज्या r है, एक दूसरे को स्पर्श करते हैं, तो उस वृत्त की त्रिज्या जो दिये गये तीनों वृत्तों को अन्तः स्पर्श करता है, होगी
View SolutionProve that the circle x2+y2=a2and(x−2a)2+y2=a2 are equal and touch each other. Also find the equation of a circle (or circles) of equal radius touching both the circles.
View SolutionProve that the circle x2+y2=a2and(x−2a)2+y2=a2 are equal and touch each other. Also find the equation of a circle (or circles) of equal radius touching both the circles.
View Solutioninside the circles x2+y2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to
View Solution
