It is given that ΔDEF~ΔPQR.EF:QR=3:2, then value of ar(DEF) : ar(PQR) is
4:9
4:8
9:2
9:4
To solve the problem, we need to find the ratio of the areas of triangles DEF and PQR given that they are similar and the ratio of one pair of corresponding sides is provided.
1. Understanding Similar Triangles:
Since triangles DEF and PQR are similar (denoted as ΔDEF ~ ΔPQR), we know that the ratios of their corresponding sides are equal.
2. Given Ratio of Sides:
We are given the ratio of the sides EF and QR as 3:2. This can be expressed as:
EFQR=32
3. Using the Area Ratio Theorem:
The theorem states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(DEF)ar(PQR)=(EFQR)2
4. Substituting the Given Ratio:
Now, we substitute the given ratio of EF to QR into the equation:
ar(DEF)ar(PQR)=(32)2
5. Calculating the Square:
Calculate the square of the ratio:
(32)2=94
6. Final Ratio of Areas:
Thus, we have:
ar(DEF)ar(PQR)=94
Conclusion:
The ratio of the areas of triangles DEF and PQR is:
ar(DEF):ar(PQR)=9:4
Since triangles DEF and PQR are similar (denoted as ΔDEF ~ ΔPQR), we know that the ratios of their corresponding sides are equal.
We are given the ratio of the sides EF and QR as 3:2. This can be expressed as:
EFQR=32
The theorem states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(DEF)ar(PQR)=(EFQR)2
Now, we substitute the given ratio of EF to QR into the equation:
ar(DEF)ar(PQR)=(32)2
Calculate the square of the ratio:
(32)2=94
Thus, we have:
ar(DEF)ar(PQR)=94
The ratio of the areas of triangles DEF and PQR is:
ar(DEF):ar(PQR)=9:4
Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-B
20 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
42 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 STANDARDBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 STANDARDEXERCISE - SECTION-C (CASE STUDY)
10 Videos
Similar Questions
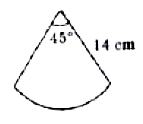
The perimeter of the sector of a circle of radius 14 cm and central angle 45∘ is
View SolutionSukriti throws a ball upwards , from a rooftop which is 8 m high from ground level . The ball reaches to some maximum height and then returns and hit the ground .
It height of the ball at time t (in sec) is represented by h(m) , then equation of its path is given as h=−t2+2t+8
Based on above information , answer the following

The maximum height achieved by ball is
View SolutionThe value(s) of k for which the quadratic equation 2x2+kx+2=0 has equal roots, is
View SolutionA book store shopkeeper gives books on rent for reading. He has variety of books in his store related to fiction , stories and quizzes etc. He takes a fixed charge for the first two days and an additional charges for subsequent day . Amruta paid Rs 22 for a book and kept for 6 days, while Radhika paid Rs 16 for keeping the books for 4 days.

Assume that the fixed charge be rs x and additional charge (per day) by Rs y.
Based on the above information answer and four of the following questions:
The situation of amount paid by Radhika is algebraically repesented by .
View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
View SolutionIn ΔABCandΔDEF, we have ABDE=BCEF=ACDF=57, then ar(ΔABC):ar(ΔDFR)=?
View SolutionΔABC~ΔDEC such that ar(ΔABC)=64cm2andar(ΔDEF)=169cm2. If BC=4cm, find EF.
View SolutionΔABC में AC -6 सेमि तथा भुजा AC के तदनुरूपी शीर्षलम्ब =4 सेमि है | ΔDEF में EF =8 सेमि है |यदि ar(ΔABC)=ar(ΔDEF) हो तो भुजा EF के तदनुरूपी शीर्षलम्ब ज्ञात करें|
View SolutionΔABC में AB=8 सेमी तथा AB के संगत शीर्षलम्ब 5 सेमी है ΔDEF में EF=10 सेमी। यदि ar(ΔABC)=ar(ΔDEF) तब EF के संगत शीर्षलम्ब ज्ञात कीजिए।
View Solutionदो त्रिभुजें ABC और DEF इस प्रकार है की ar(ΔABC)=9 वर्ग सेमि तथा ar(ΔDEF)=16 वर्ग सेमि. है |यदि ΔABC~ΔDEF और BC = 2 .1 सेमि हो तो EF का मान ज्ञात करो|
View Solutionदो त्रिभुजें ABC और DEF इस प्रकार है की AB =5सेमि., ar(ΔABC)=20 सेमि 2 तथा ar(ΔDEF)=45 सेमि 2 यदि ΔABC~ΔDEF हो तो DF का मान ज्ञात करो|
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि ABDE=BCEF=CAFD=25 तो ar(ΔABC):ar(ΔDEF)=
View Solutionयह दिया है कि BCQR=13 के साथ ΔABC~ΔPQR है I तब ar(PQR)ar(ABC) बराबर है :
View SolutionIf ΔABC~ΔPQR with BCQR=13, then find arΔPRQarΔBCA ?
View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View Solutionसमकोण ΔPQR और ΔDEF में यदि कर्ण, PQ = कर्ण EF और PR = भुजा DE भुजा तो ΔPQR≅Δ.
View Solution
