Let A and B be two events such that p(¯¯¯A∪B)=16,p(A∩B)=14 and p(¯¯¯A)=14 , where ¯¯¯A stands for the complement of the event A. Then the events A and B are (1) mutually exclusive and independent (2) equally likely but not independent (3) independent but not equally likely (4) independent and equally likely
equally likely but not independent equally likely and mutually exclusive
equually like and mutually exclusive
Mutually exclusive and independent
independent but not equally likely
The correct Answer is:D
We have, P(¯¯¯¯¯¯¯¯¯¯A∪B)=14,P(A∩B)=14
P(¯¯¯A)=14⇒P(A)=1−14=34
∴P(¯¯¯¯¯¯¯¯¯¯A∪B)=1−P(a∪B)=1−[P(A)+P(B)−P(A∩B)]
⇒⇒16=1−34−P(B)+14
⇒P(B)=1−12−16=6−3−16=26=13
Since P(A∩B)=P(A)P(B)andP(A)≠P(B), therefore A and B are independent but not equally likely.
Similar Questions
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14 where ¯¯¯A stands for complement of event A. Then, events A and B are
View SolutionLet A and B be two events such that
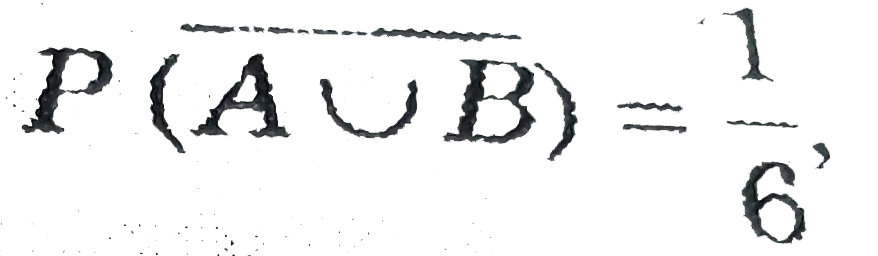
,P(A∩B)=14 and P−A=14, where −A stands for the complement of the event A. Then, the events A and B are
View Solution
Knowledge Check
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCIndependent but not equally likelyDindependent and equally likelyLet A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCindependent but not equally likelyDindependent and equally likelyIf A and B are any two events such that P(A∪B)=34,
P(A∩B)=14andP(¯¯¯A)=23, where ¯¯¯A stands for the complementary event of A, then what is P(B) ?A13B23C19D29
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View SolutionLet A and B be events such that P(¯¯¯A)=45,P(B)=13,P(AB)=16 then
View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩B)
View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩B)
View SolutionLet A and B be independent events such that P(A) =0.6 and P(B ) =0.4.
find P(A∩¯¯¯B)
View Solution
