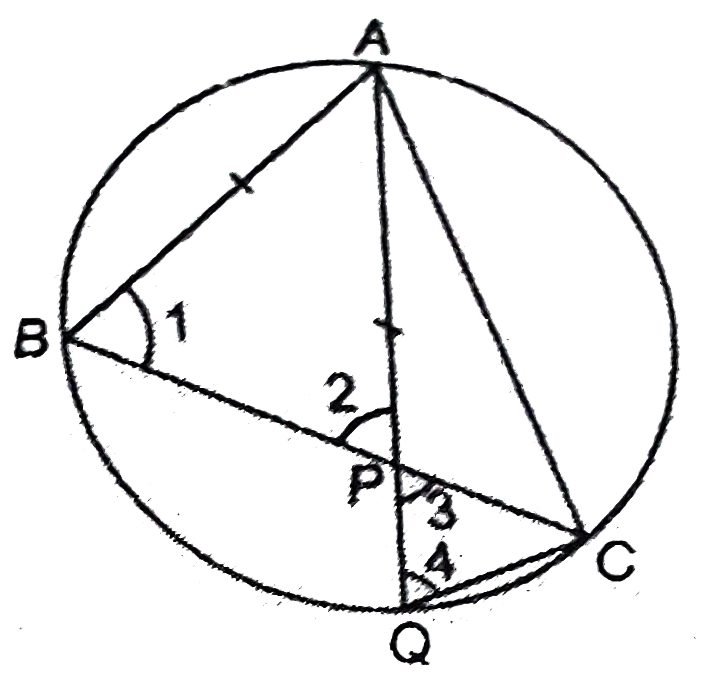
Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC

In the figure, altitude AD meets BC at D and circumcircle at P. In circumcircle of triangle ABC, chord AB subtends same angle at point C and P.
∴Ang≤BPA=∠BCA=C
i.e., ∠BPD=C
Also ∠HBD=90∘−C∴∠BHD=C
Thus ΔBPDandΔBHD are similar.
∴HD=DP
Therefore, P is image of H in BC
Also, HP=2HD=2(2RcosBcosC)
=4RcosBcosC
Topper's Solved these Questions
Similar Questions
Let Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionIf H is the orthocentre of a acute-angled triangle ABC whose circumcircle is x2+y2=16 then circum diameter of the triangle HBC is
View SolutionIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠BCD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠DCI
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠BIC
View SolutionIn given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
View Solution

