Let f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt.
y=f(x) is Solution in Bengali
The curve y=f(x) passes through the point (1,2)
The curve y=f(x) passes through the point (2,-1)
The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−24
The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−14
The correct Answer is:B, C
f(x)=1−2x+x∫0ex−1f(t)dt
⇒ f(x)=1−2x+exx∫0e−tf(t)dt ...(i)
Differentiating w.r.t. x, we get
f'(x)=−2+exe−xf(x)+exx∫0e−tf(t)dt ...(ii)
Subtracting (i) from (ii), we get
f'(x)−f(x)=−2+f(x)−1+2x
⇒ f'(x)−2f(x)=2x−3
This is linear differential equation.
I.F.=e∫−2dx=e−2x
Therefore, solution is
y⋅e−2x=∫(2x−3)e−2xdx+c
⇒ y⋅e−2x=(2x−3)⋅e−2x−2−∫2×e−2x−2dx+c
⇒ y⋅e−2x=−(2x−3)e−2x2−e−2x2+c
⇒ y⋅e−2x=(1−x)e−2x+c
⇒ y=(1−x)+c.e2x ...(iii)
Putting x=0 in (i), we get f(0)=1.
So, from above equation, we have
1=1+c⇒c=0
Now, (iii) reduces to y=1-x, which passes through point (2,-1).
Now,f(x)≤y≤√1−x2
⇒ 1−x≤y≤√1−x2
1−x≤y represents the region above the line 1−x=yandy≤√1−x2 represents the region inside the semicircle (lying above x-axis) x2+y2=1.
So, common region is as the shaded one in the following figure :
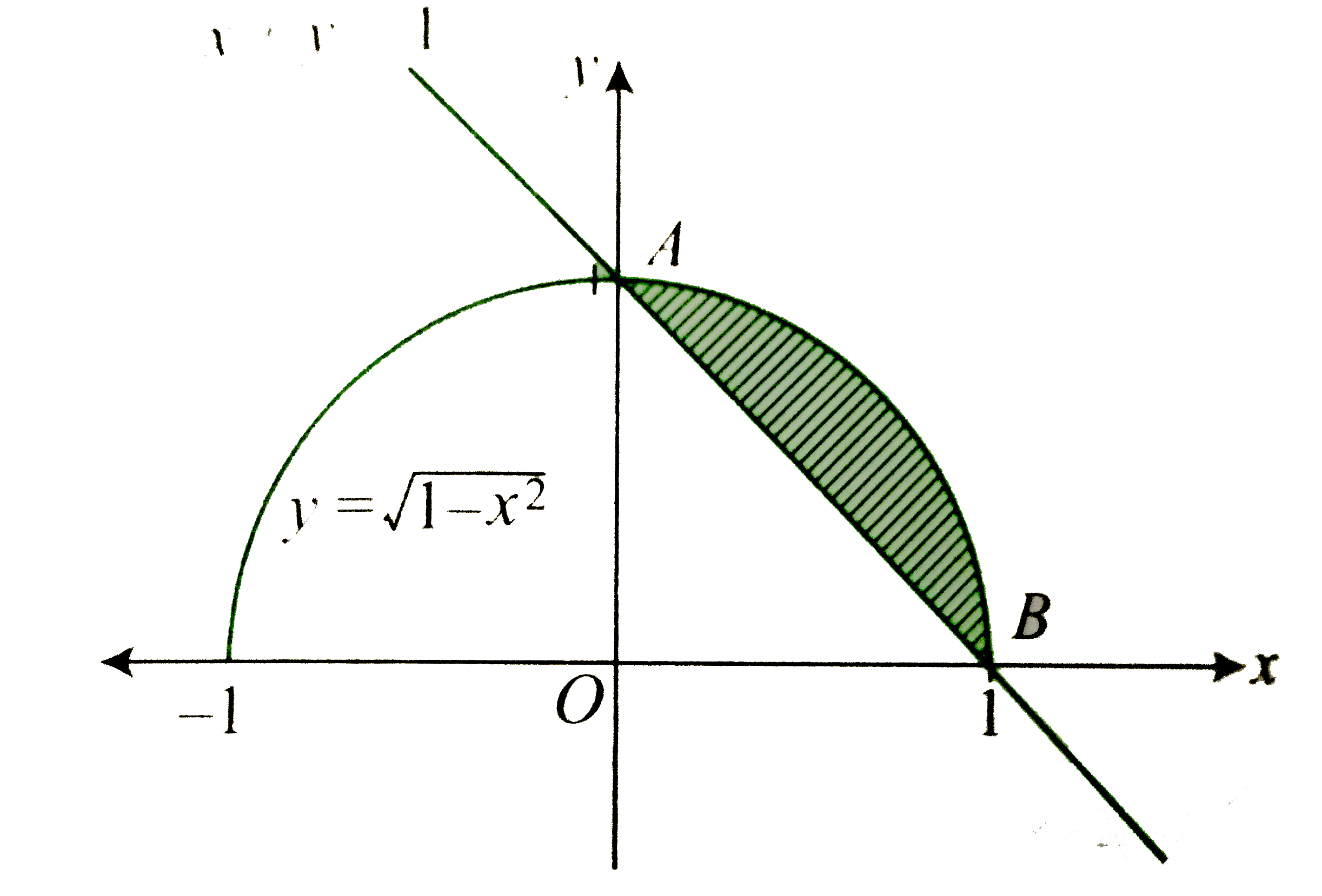
Area of the shaded region
=Area of quarter of the circle - Area of triangle OAB
=14×π(1)2−12×1×1=π−24
Topper's Solved these Questions
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Linkded Comprehension Type
Explore 18 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Matrix Match Type
Explore 4 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Exercises - Single Correct Answer Type
Explore 40 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:Comprehension Type
Explore 3 Videos
- BINOMIAL THEOREMBook:CENGAGE PUBLICATIONChapter:BINOMIAL THEOREMExercise:Comprehension
Explore 11 Videos
Similar Questions
Let Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionMatch the following lists :

View SolutionArea enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2isequa<o πsq.units (b) π2sq.units 3π4sq.units (d) 3π2sq.units
View SolutionLet f(x) be a function such that its derovative f'(x) is continuous in [a, b] and differentiable in (a, b). Consider a function ϕ(x)=f(b)−f(x)−(b−x)f'(x)−(b−x)2A. If Rolle's theorem is applicable to ϕ(x) on, [a,b], answer following questions.
If there exists some unmber c(a lt c lt b) such that ϕ'(c)=0andf(b)=f(a)+(b−a)f'(a)+λ(b−a)2f''(c), then λ is
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionLet f(x) be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt then ∫10f(x)dx=
View SolutionLet f be a differentiable function such that f(x)=x^(2)+int_(0)^(x)e^(-t)f(x-t)dt then prove that f(x)=(x^(3))/(3)+x^(2)
View Solutionif f be a differentiable function such that f(x)=x2∫x0e−tf(x−t). dt. Then f(x) =
View SolutionLet f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt.
f(x) increases for
View SolutionLet f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt.
y=f(x) is
View SolutionLet y=f(x) satisfies the equation f(x)=(e−x+ex)cosx−2x−∫x0(x−t)f′(t)dt y satisfies the differential equation
View SolutionLet y=f(x) satisfies the equation
f(x)=(e−x+ex)cosx−2x+∫x0(x−t)f′(t)dt
The value of f(0)+f′(0) equal
View SolutionIf f(x) is differentiable function and f(x)=x2+∫x0e−t(x−t)dt,then f)-t) equals to
View SolutionLet y=f(x) satisfies the equation f(x)=(e−x+ex)cosx−2x−∫x0(x−t)f'(t)dt. The value of f'(0)+f''(0)equals to
View SolutionLet f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt.
y=f(x) is
View SolutionLet y=f(x) satisfies the equation f(x)=(e−x+ex)cosx−2x−∫x0(x−t)f′(t)dt y satisfies the differential equation
View Solution
