Let f(x)=x−[x] , for every real number x (where, [x] is integral part of x). Then , the value of ∫1−1f(x)dx is equal to
1
2
0
1/2
The correct Answer is:A
We have,
1∫−1(x−[x])dx=0∫−1(x−[x])dx+1∫0(x−[x])dx
1∫−1(x−[x])dx=0∫−1(x+1)dx+1∫0(x−0)dx
1∫−1(x−[x])dx=[(x+1)22]0−1+[x22]10=12+12=1
ALTER It is evident from the graph of y=f(x) that
1∫−1dx=Area of ΔOLA+Area of ΔOMB
⇒1∫−1f(x)dx=2(Area ofΔOMB)
⇒1∫−1f(x)dx=2×12(OM×MB)=1×1=1
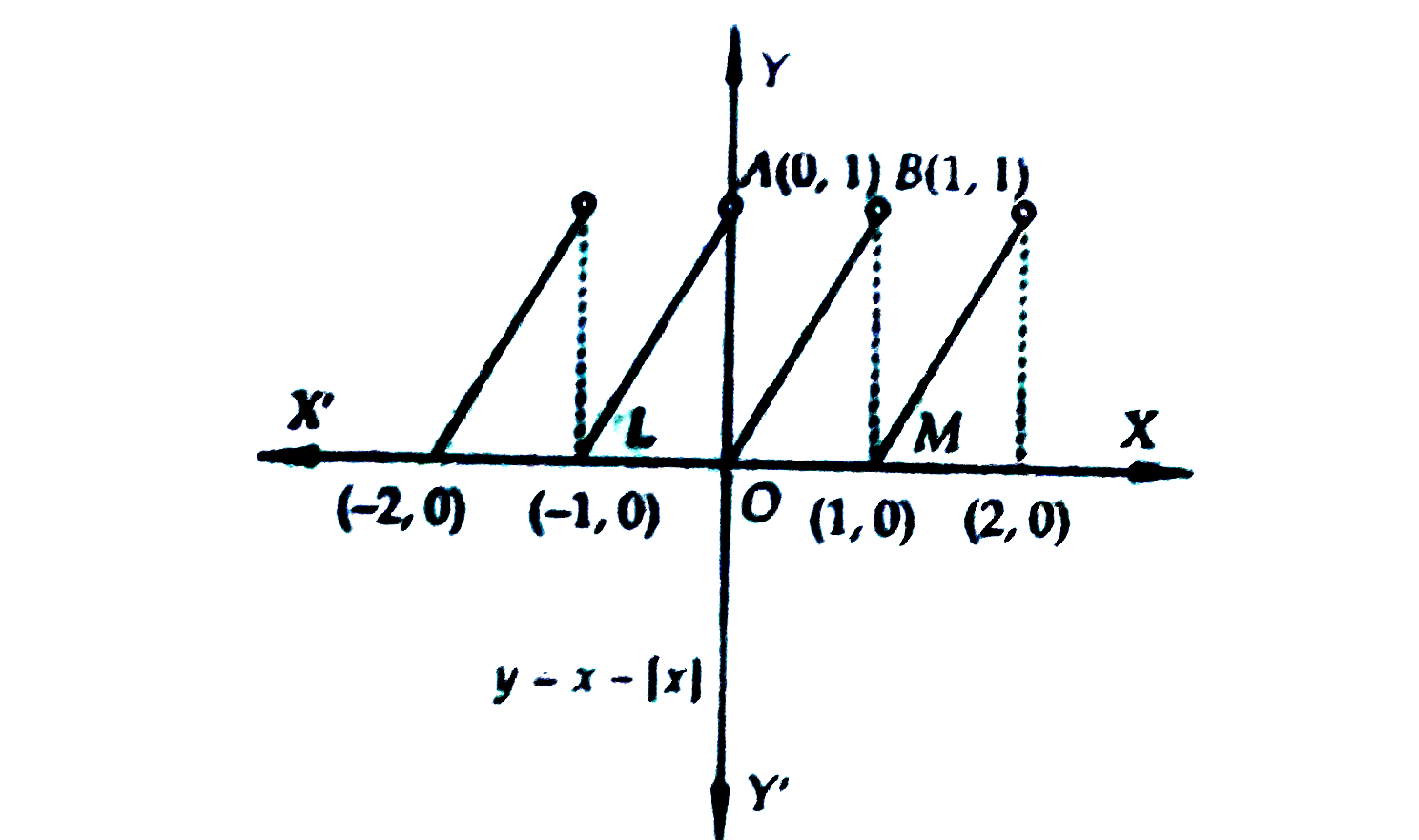
Topper's Solved these Questions
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Section I - Solved Mcqs
Explore 144 Videos
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Section II - Assertion Reason Type
Explore 12 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:OBJECTIVE RD SHARMA ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise
Explore 87 Videos
- DERIVATIVE AS A RATE MEASURER Book:OBJECTIVE RD SHARMA ENGLISHChapter:DERIVATIVE AS A RATE MEASURER Exercise:Exercise
Explore 26 Videos
Similar Questions
∫100|x(x−1)(x−2)|dx is equal to
View SolutionStatement-1: ∫π/20xcotxdx=π2log2
Statement-2: ∫π/20logsinxdx=−π2log2
View SolutionThe function f(x)=4−x24x−x3 is discontinuous at
View SolutionThe edge of a cube is equal to the radius of a sphere. If the edge and the radius increase at the same rate, then the ratio of the increases in surface areas of the cube and sphere is
View SolutionGiven a function f(x) such that It is integrable over every interval on the real line, and f(t+x)=f(x), for every x and a real t. Then show that the integral ∫a+taf(x)dx is independent of a.
View SolutionLet f(x)=x−[x], for every real number x, where [x] is integral part of x. Then ∫1−1f(x)dx is
View SolutionLet f be a real valued continuous function on R . (the set all real numbers) and satisfying f(x)=x^(2)+int_(-1)^(1)(x+y)f(y)dy where x and y are independent variables.f(x)>k for every real x,then the largest integral value of k is
View SolutionLet f(x)=x[x], for every real number x , where [x] is the greatest integer less than or equal to x. Then,evaluate int_(-1)^(1)f(x)dx
View SolutionLet f(x)=int_(3)^(25n+(1)/(4))e^({2x+3})dx, where {x} is fractional part of x, then f(x) is equal to
View SolutionIf f(a+b+1−x)=f(x), for all x where a and b are fixed positive real numbers, the 1a+b∫bax(f(x)+f(x+1)) dx is equal to :
View SolutionIf f(x) is an integrable function over every interval on the real line such that f(t+x)=f(x) for every x and real t, then
∫a+1af(x)dx is equal to
View Solution∫2−1f(x)dx where f(x)=|x+1|+|x|+|x−1| is equal to
View Solutionमाना f(x)=x−[x] सभी वास्तविक संख्याओं x के लिए, जहाँ [x],x का समाकलनीय खण्ड है तो ∫1−1f(x)dx है।
View SolutionLet f(x)=x−[x], for every real number x, where [x] is integral part of x. Then ∫1−1f(x)dx is:
View SolutionLet f(x)={x}, the fractional part of x then ∫1−1f(x)dx is equal to
View SolutionIf f(a+b+1−x)=f(x), for all x where a and b are fixed positive real numbers, the 1a+b∫bax(f(x)+f(x+1) dx is equal to :
View Solution
