Let 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
4l2=2b2+2c2−a2
4l2=b2+c2+2bccosA
4l2=a2+4bccosA
4l2=(2s−a)2sin2A2
The correct Answer is:A, B, C, D
To find the length of the median l from vertex A to side BC in triangle ABC, we can use the Apollonius theorem. The theorem states that:
AB2+AC2=2AD2+2BD2
where D is the midpoint of side BC.
1. Identify the sides of the triangle:
Let AB=c, AC=b, and BC=a. Since D is the midpoint of BC, we have BD=DC=a2.
2. Apply the Apollonius theorem:
According to the theorem, we can write:
c2+b2=2l2+2(a2)2
Simplifying the right side:
c2+b2=2l2+2(a24)=2l2+a22
3. Rearranging the equation:
Rearranging gives us:
2l2=c2+b2−a22
4. Divide by 2:
Dividing both sides by 2 to isolate l2:
l2=c2+b2−a222
5. Final expression for l:
Taking the square root gives us:
l=
⎷c2+b2−a222
Conclusion:
Thus, the length of the median l from vertex A to side BC is given by:
l=
⎷b2+c2−a222
Let AB=c, AC=b, and BC=a. Since D is the midpoint of BC, we have BD=DC=a2.
According to the theorem, we can write:
c2+b2=2l2+2(a2)2
Simplifying the right side:
c2+b2=2l2+2(a24)=2l2+a22
Rearranging gives us:
2l2=c2+b2−a22
Dividing both sides by 2 to isolate l2:
l2=c2+b2−a222
Taking the square root gives us:
l=
⎷c2+b2−a222
Thus, the length of the median l from vertex A to side BC is given by:
l=
⎷b2+c2−a222
Topper's Solved these Questions
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGE ENGLISHChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Comprehension Type
Explore 6 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE Book:CENGAGE ENGLISHChapter:SOLUTIONS AND PROPERTIES OF TRIANGLE Exercise:Comprehension Type
Explore 6 Videos
- SET THEORY AND REAL NUMBER SYSTEM Book:CENGAGE ENGLISHChapter:SET THEORY AND REAL NUMBER SYSTEM Exercise:Archives
Explore 1 Video
- STATISTICSBook:CENGAGE ENGLISHChapter:STATISTICSExercise:Archives
Explore 10 Videos
Similar Questions
In ΔABC,'h' is the length of altitude drawn from vertex A on the side BC. Prove that:
2(b2+c2)≥4h2+a2. Also, discuss the case when equality holds true.
View SolutionTwo sides of a triangle are to have lengths 'a'cm & 'b'cm. If the triangle is to have the maximum area, then the length of the median from the vertex containing the sides 'a' and 'b'is
View SolutionLet the lengths of the altitudes drawn from the vertices of ΔABC to the opposite sides are 2, 2 and 3. If the area of ΔABC is Δ, then find the area of triangle
View SolutionLet position vectors of point A,B and C of triangle ABC represents be ˆi+ˆj+2ˆk,ˆi+2ˆj+ˆk and 2ˆi+ˆj+ˆk. Let l1+l2 and l3 be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then (l1+l2+l3) equals
View SolutionLet position vectors of point A,B and C of triangle ABC represents be ˆi+ˆj+2ˆk,ˆi+2ˆj+ˆk and 2ˆi+ˆj+ˆk. Let l1,l2 and l3 be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then (l1+l2+l3) equals
View SolutionThe slope of a median, drawn from the vertex A of the triangle ABC is -2. The co-ordinates of vertices B and C are respectively (-1, 3) and (3, 5). If the area of the triangle be 5 square units, then possible distance of vertex A from the origin is/are.
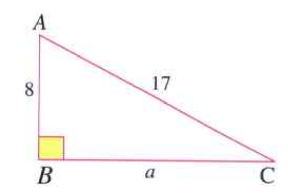
View SolutionFind the length of side BC in the given triangle.
View SolutionLet f,gandh be the lengths of the perpendiculars from the circumcenter of ΔABC on the sides a, b, and c, respectively. Prove that af+bg+ch=14abcfgh
View SolutionIf in ΔABC,b=3cm,c=4cm and the length of the perpendicular from A to the side BC is 2 cm, then how many such triangle are possible ?
View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View Solution
