Let P(sinθ,cosθ) (0≤θ≤2π) be a point and let OAB be a triangle with vertices (0,0),(√32,0)and(0,√32) Find θ if P lies inside △OAB
0<0<π/12
5π/2<θ<π/2
0<θ<5π/2
5π/2<θ<π
The correct Answer is:A, B
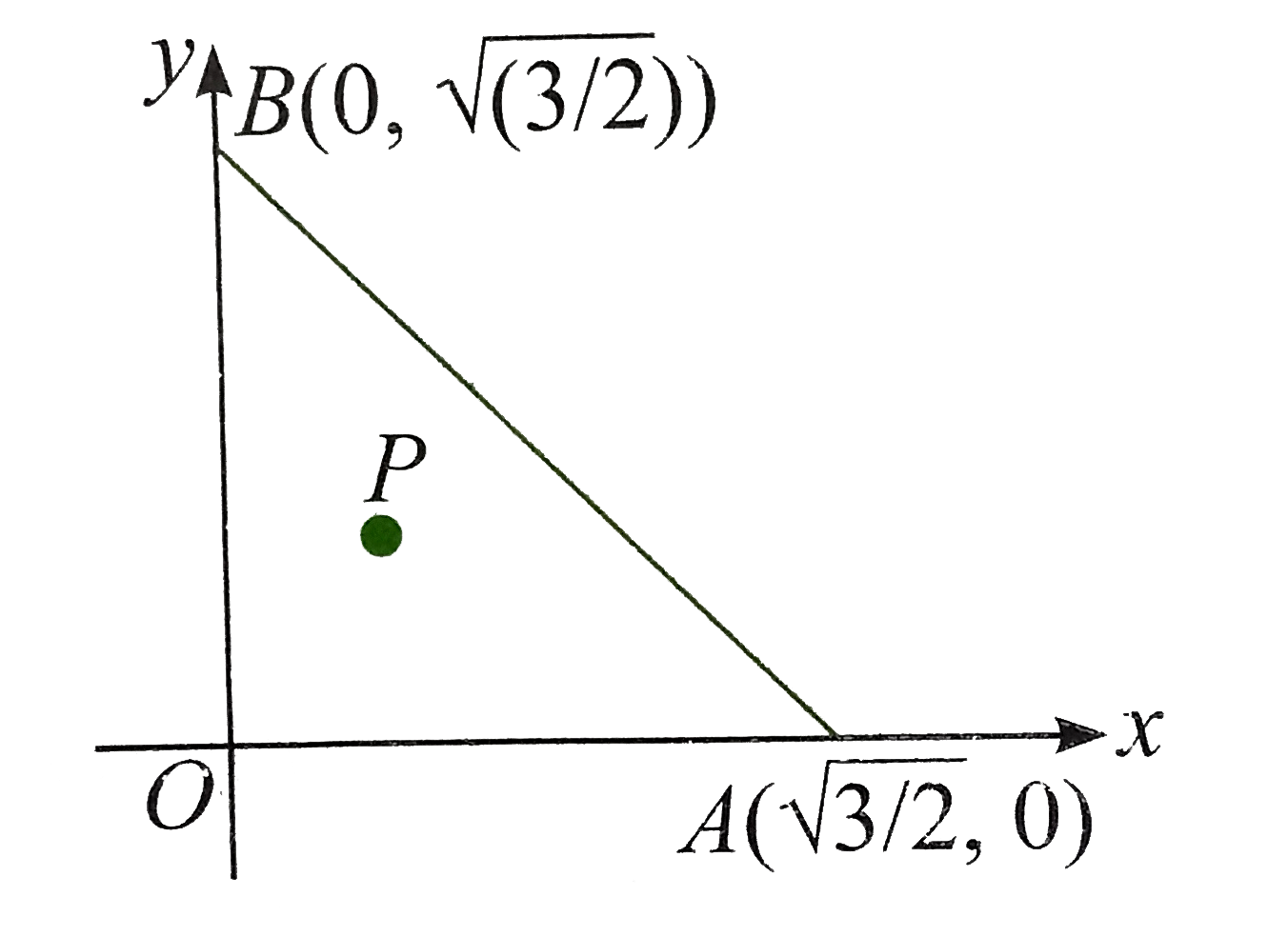
The equations of lines along OA, OB and AB are y=0, x=0, and x+y =√3/2, respectively.
Now, P and B will lie on the same side of y=0 if cosθ>0. Similarly, P and A will lie on the same side of x=0 if sin θ>0, and P and O will lie on the same side of x+y=√3/2 if sin θ+cosθ<√3/2. Hence, P will lie inside ΔABCif sinθ>0,cos θ>0, and sin θ+cos θ<√3/2, Now,
sin θ+cos θ<√32
or sin(θ+π4)<√34
Since sin θ>0 and cos θ>0,0<θ<π/12 or 5π/12<θ<π/2.
Similar Questions
Let P (sin theta, cos theta) (0 le theta le 2pi) be a point and let OAB be a triangle with vertices (0,0) , (sqrt(3/2),0) and (0,sqrt(3/2)) Find theta if P lies inside triangle OAB.
View SolutionLet P(sinθ,cosθ) (0≤θ≤2π) be a point and let OAB be a triangle with vertices (0,0),(√32,0)and(0,√32) Find θ if P lies inside △OAB
View Solutionमाना P(sinθ,cosθ)(0≤θ≤2π) एक बिन्दु है तथा माना OAB एक त्रिभुज है, जिसके शीर्ष (0,0),(√32,0) तथा (0,√32) है। यदि P,ΔOAB के अन्दर स्थित है, तो θ ज्ञात कीजिए।
View SolutionP(sinθ,cosθ)(0≤θ≤2π) बिंदु (0,0),(√3/2,0) और (0,√3/2) से बनने वाले त्रिभुज के अंदर स्थित है यदि-
View SolutionP(sinθ,cosθ)(0≤θ≤2π) बिंदु (0,0),(√3/2,0) और (0,√3/2) से बनने वाले त्रिभुज के अंदर स्थित है यदि-
View SolutionIf 2 cos2θ+sinθ−2=0and0∘≤θ≤90∘ find the value of θ.
View SolutionLet P(sinθ,cosθ) (0≤θ≤2π) be a point and let OAB be a triangle with vertices (0,0),(√32,0)and(0,√32) Find θ if P lies inside △OAB
View SolutionLet P (sin theta, cos theta) (0 le theta le 2pi) be a point and let OAB be a triangle with vertices (0,0) , (sqrt(3/2),0) and (0,sqrt(3/2)) Find theta if P lies inside triangle OAB
View Solution
