Letf:R→R and g:R→R be respectively given by f(x)=|x|+1andg(x)=x2+1. Define h:R→R by
h(x)={max{f(x),g(x)}ifx≤0min{f(x),g(x)}ifx>0
The number of points at which h(x) is not differentiable isSolution in Bengali
First we draw the graph, of y=|x|+1andy=x2+1
y=|x|+1={x+1,x≥0−x+1,x<0
y=x2+1 is a parabola having vertex at (0, 1) and concave upwards
Thus, the graphs of both functions are as shown in the following figure.
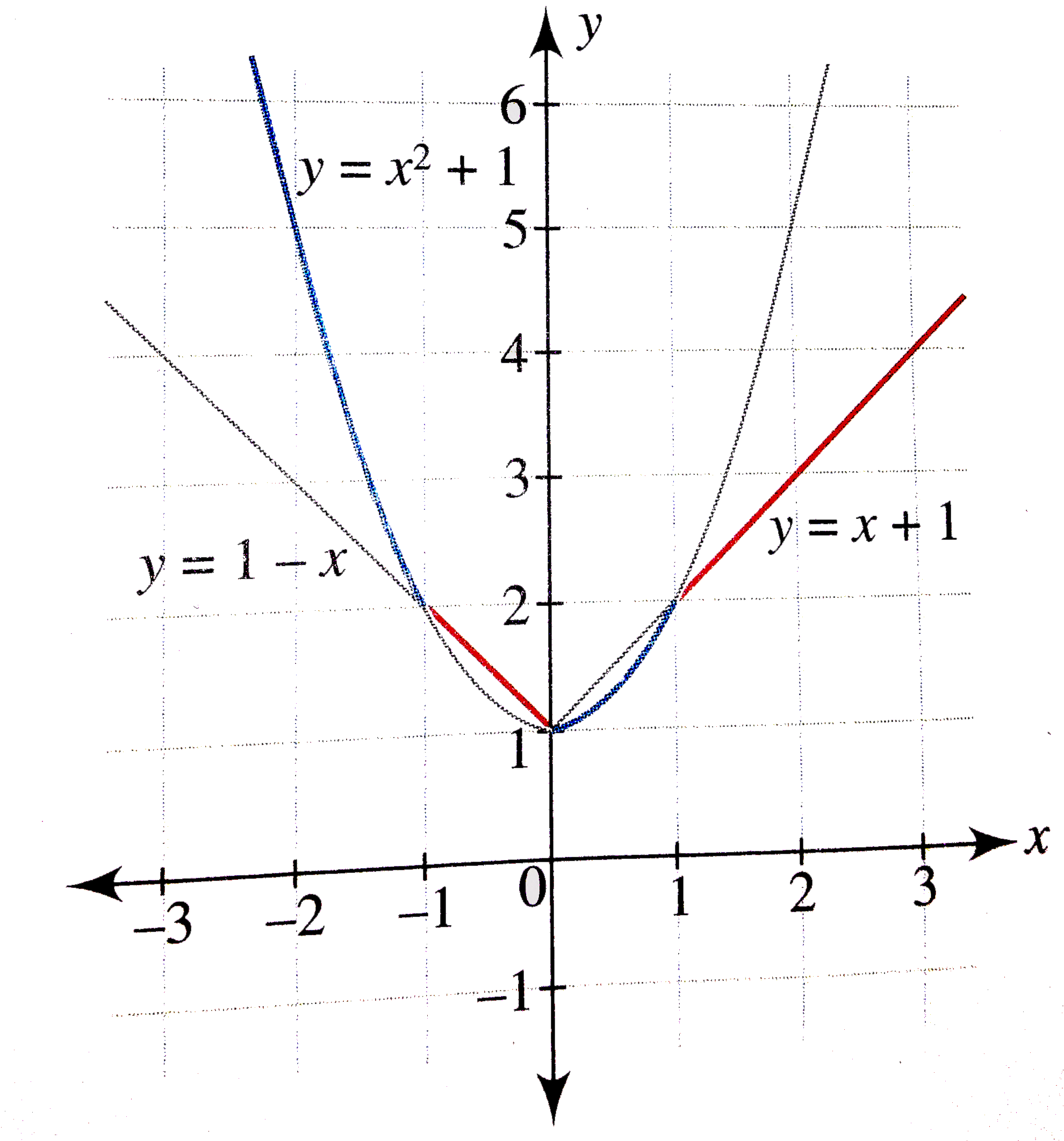
From the graph, the required function is
h(x)=⎧⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪⎩x2+1,x∈(−∞,−1)−x+1,x∈[−1,0)x2+1,x∈[0,1)x+1,x∈[1,∞)
which is non-different at x=−1,0and1.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGE PUBLICATIONChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:EXERCISES
Explore 33 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGE PUBLICATIONChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercises
Explore 16 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGE PUBLICATIONChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercises
Explore 22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f:R rarr R and g:R rarr R be respectively given by f(x)=|x|+1 and g(x)=x^(2)+1. Define h:R rarr R by h(x)={max{f(x),g(x)},quad if x 0 The number of points at which h(x) is not differentiable is
View SolutionLet f(x)={x-1,-1<=x<0 and x^(2),0<=x<=1,g(x)=sin x and h(x)=f(|g(x)|)+[f(g(x)) Then
View SolutionLet the function f, g, h are defined from the set of real numbers RR to RR such that f(x) = x^2-1, g(x) = sqrt(x^2+1), h(x) = {(0, if x lt 0), (x, if x gt= 0):}. Then h o (f o g)(x) is defined by
View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f be a twice differentiable function such that
f''(x)=−f(x) and f'(x)=g(x).If h'(x)=[f(x)]2+[g(x)]2,
h(a)=8 and h(0)=2, then h(2)=
View SolutionLet f:R→R and g:R→R be respectively given by f(x)=|x|+1 and g(x)=x2+1. Define h:R→R by
h(x)={max{f(x),g(x)}ifx≤0min{f(x),g(x)}ifx>0
The number of points at which h(x) is not differentiable is :
View SolutionLet f:R→R be defined by f(x)=−x3+x,g:[−1,1]→Randh:[−1,1]→R is defined by g(x) = min(fx),0), h(x) = max(f(x),0)
Number of roots of the g(x)=−12 is____
View SolutionLet f(x) = {{:(x + 1 , :, x £ 0) , (x , : , x gt 0):} and h (x) = |f(x) + f(|x|) . Then h(x) is defined by :
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) : g(x) এর পাল্লা হয় -
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) :g(x)=−12 সমীকরণের বীজসংখ্যা হয় -
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) : নীচের কোনটি যুগ এবং অযুগ্ম উভয় অপেক্ষকই?
View SolutionIf f(x)=(g(x))+g(−x)2+2[h(x)+h(−x)]−1 where g and h are differentiable functions then f'(0)
View SolutionLet f(x) be defined on [−2,2] and be given by f(x)={−1;−2≤x≤0} andf(x)={x−1;0<x≤2}.andg(x)=f(|x|)+|f(x)| Find g(x)
View Solution
