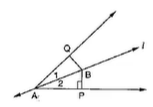
Line l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
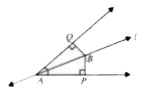
ΔAPB≅ΔAQB
Step by step video solution for Line l is the bisector of an angleA and B is any point on I. BP and BQ are perpendiculars from B to the arms of angleA (see figure). Show that: DeltaAPB~=DeltaAQB by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023टॉपर्स ने हल किए ये सवाल
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.2)
Explore 9 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.3)
Explore 10 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
समान प्रश्न
Line l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
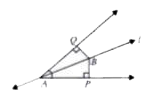
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionIn the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
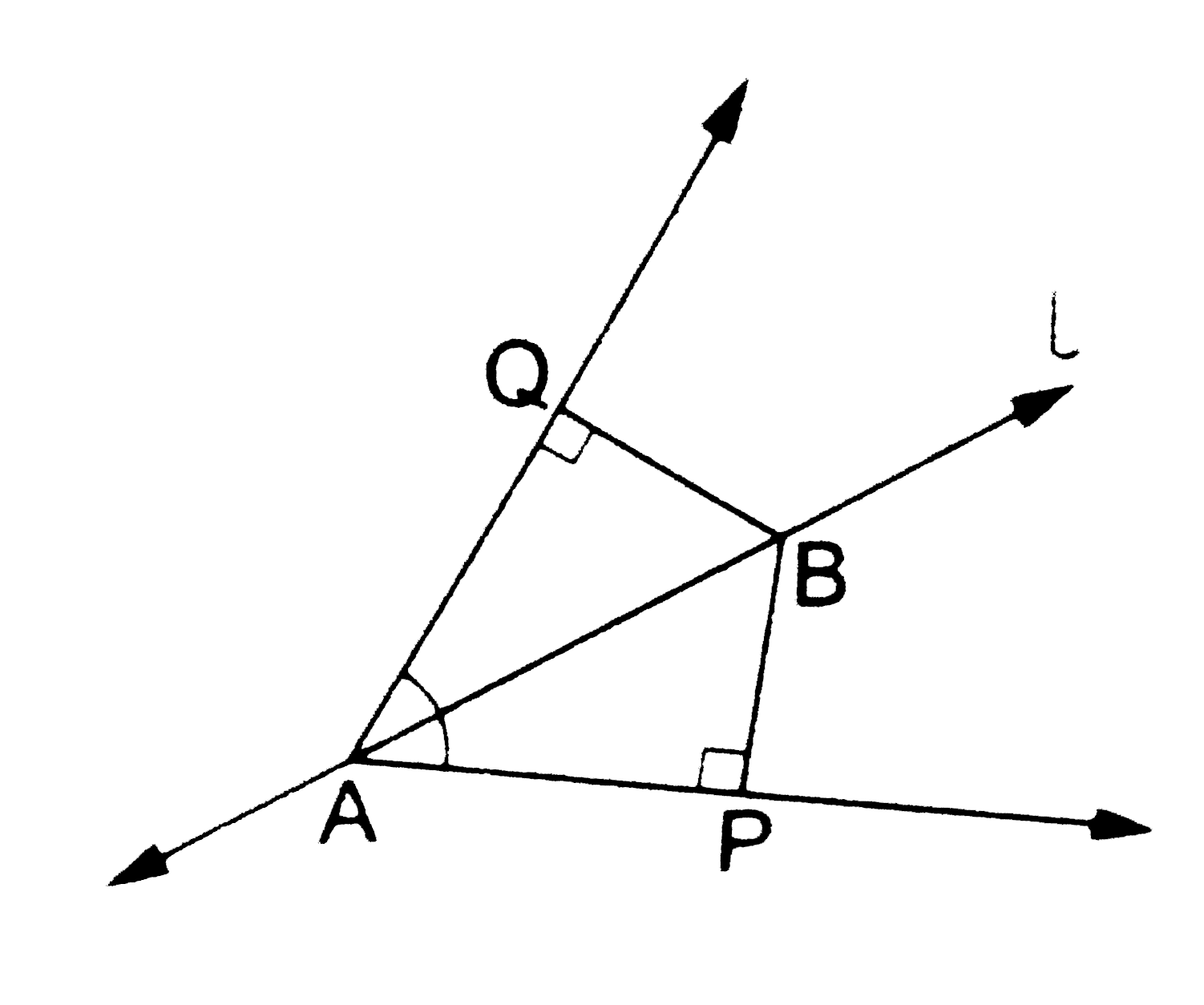
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View SolutionIn the given figure, line I is the bisector of an angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A. Show that B is equidistant from the arms of ∠A.
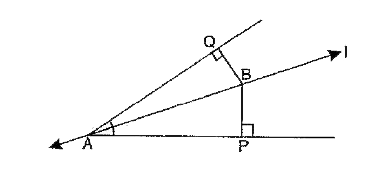
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View SolutionIn ΔABC, the bisector AD of ∠A is perpendicular to side BC (see figure). Show that AB =AC or ΔABC is isosceles.

View SolutionABCD is a rectangle (Fig. 11.31) in which DP and BQ are perpendiculars from D and B respectively on diagonal AC. Show that(1) ΔADP=ΔACBQ (ii) ∠ADP=∠CBQ(iii) DP = BQ
View SolutionIn ΔABC, the bisector of ∠A interseats BC at D. A perpendicular to AD from B intersects AD at E. A line segment through E and parallel to AC intersects BC at G and AB at H. If AB = 26, BC = 28, AC = 30. Find the measure of DG.
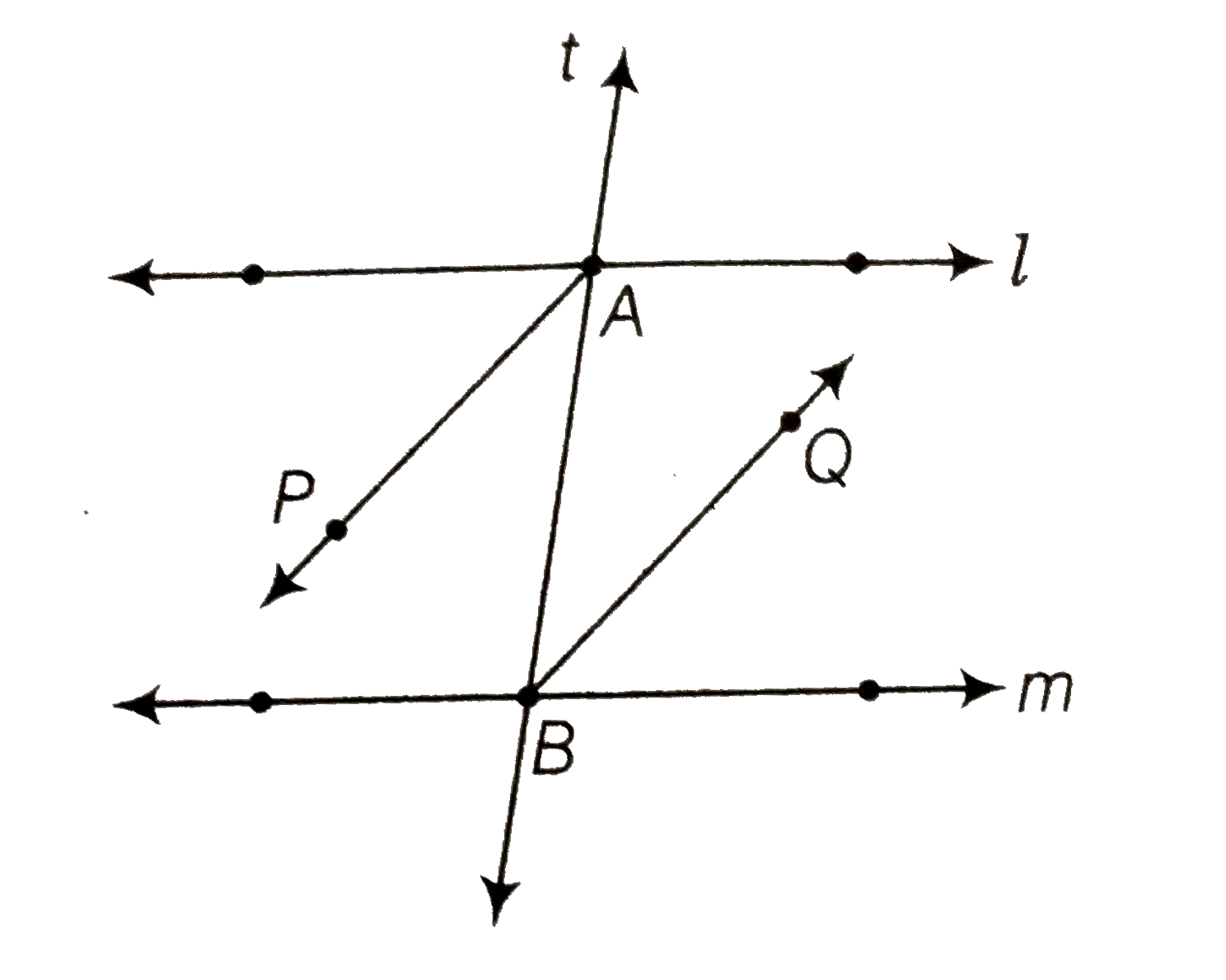
View SolutionAP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
View Solution