Lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
Video Solution
Text Solution
∠POR+∠ROQ=180o
(Linear pair of angles)
But ∠POR:∠ROQ=5:7 (Given)
Therefore, ∠POR=512×180=75o
Similarly,∠ROQ=712×180=105o
Now, ∠POS=∠ROQ=105o
(Vertically opposite angles)
and ∠SOQ=∠POR=75o
(Vertically opposite angles)
|
Similar Questions
Knowledge Check
If bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D at R and of ∠Dand∠A at S, then PQRS is a
ArectangleBrhombusCparallelogramDquadrilateral whose opposite angles are supplementaryP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘When two forces of magnitude P and Q are perpendicular to each other, their resultant is of magnitude R. When they are at an angle of 180∘ to each other, their resultant is of magnitude R√2. Find the ratio of P and Q.
A√3±2B2±√3C3±√5D5±√3
In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

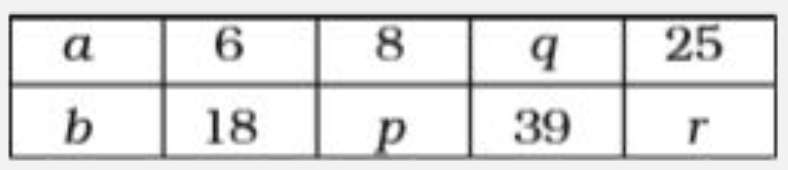
View SolutionIf a and b vary inversely to each other, then find the values of p, q, r .
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionWhen two forces of magnitude P and Q are perpendicular to each other, their resultant is of magnitude R. When they are at an angle of 180∘ to each other their resultant is of magnitude R√2 . Find the ratio of P and Q.
View Solution