Match the following lists :

Video Solution
Text Solution
a→s,b→p,c→q,d→r.
a. Since A is idempotent, we have
A2=A
⇒A3=AA2=AA=A2=A,A4=AA3=AA=A2=A
⇒An=A
⇒(I−A)n=nC0I−.nC1A+.nC2A2−.nC3A3+
=I+(−nC1+.nC2−nC3+)A
=I+[(.nC0−nC1+nC3+)−nC0]A
=I−A
b. A is involuntary. Hence,
A2=I
⇒A3=A5==A and A2=A4=A6==I
⇒(I−A)n=nC0I−nC1A+.nC2A2−nC3A3+
=nC0I−nC1A+.nC1I−.nC3A+nC4I−
=(.nC0+.nC2+.nC4+)I−(.nC1A+.nC3+.nC5+)A
=2n−1(I−A)
⇒[(I−A)n]A−1=2n−1(I−a)A−1=2n−1(A−1−I)
c. If A is nilpotent of index 2, then
A2=A3=A4=An=O
⇒(I−A)n=nC0I−.nC1A+.nC2A2−.nC3A3+
=I−nA+O+O+
=I−nA
d. A is orthogonal. Hence,
AAT=I
⇒(AT)−1=A
|
Topper's Solved these Questions
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Exercise (Numerical)
Explore 24 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:JEE Main Previous Year
Explore 11 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Exercise (Comprehension)
Explore 18 Videos
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:JEE Previous Year
Explore 10 Videos
- METHODS OF DIFFERENTIATIONBook:CENGAGEChapter:METHODS OF DIFFERENTIATIONExercise:Single Correct Answer Type
Explore 46 Videos
Similar Questions
Knowledge Check
Match the following list of microbes and their importance :
A(a)(b)(c)(d)(1)(3)(1)(4)(2)B(a)(b)(c)(d)(2)(3)(4)(1)(2)C(a)(b)(c)(d)(3)(4)(3)(2)(1)D(a)(b)(c)(d)(4)(4)(2)(1)(3)Match the following list of microbes and their importance
 AABCD3412BABCD4321CABCD4213DABCD3142
AABCD3412BABCD4321CABCD4213DABCD3142Match the following list of microbes and their importan
 AA-iv B-iii C-ii D-iBA-iv B-ii C-i D-iiiCA-iii B-i C-iv D-iiDA-iii B-iv C-i D-ii
AA-iv B-iii C-ii D-iBA-iv B-ii C-i D-iiiCA-iii B-i C-iv D-iiDA-iii B-iv C-i D-ii
Match the following list of microbes and their importance
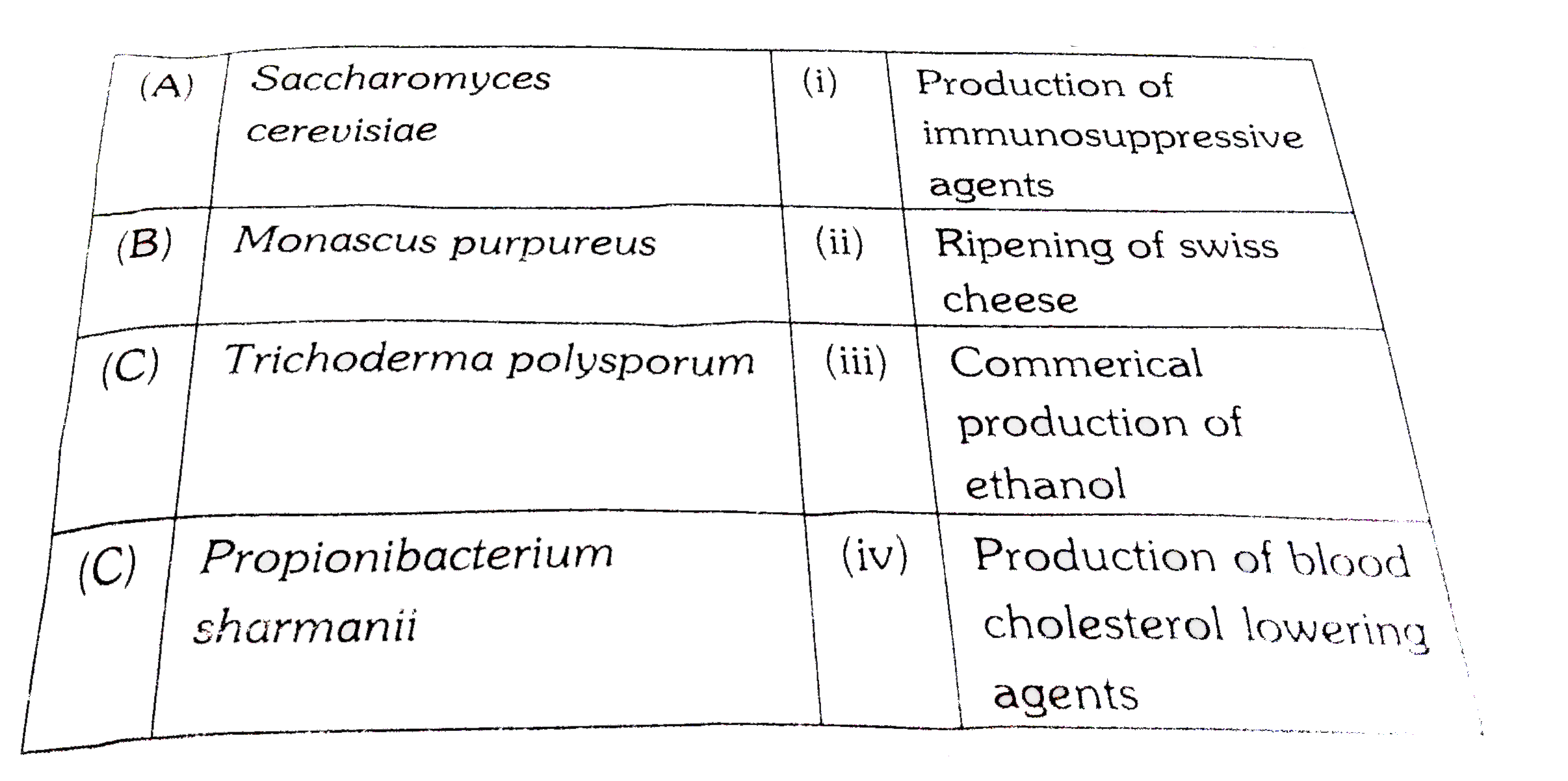
View SolutionMatch the following list of bacteria and their commereially important products:

View SolutionMatch the following list of bacteria and their commerically important products :

View SolutionMatch the following list of bacteria and their commercially important products
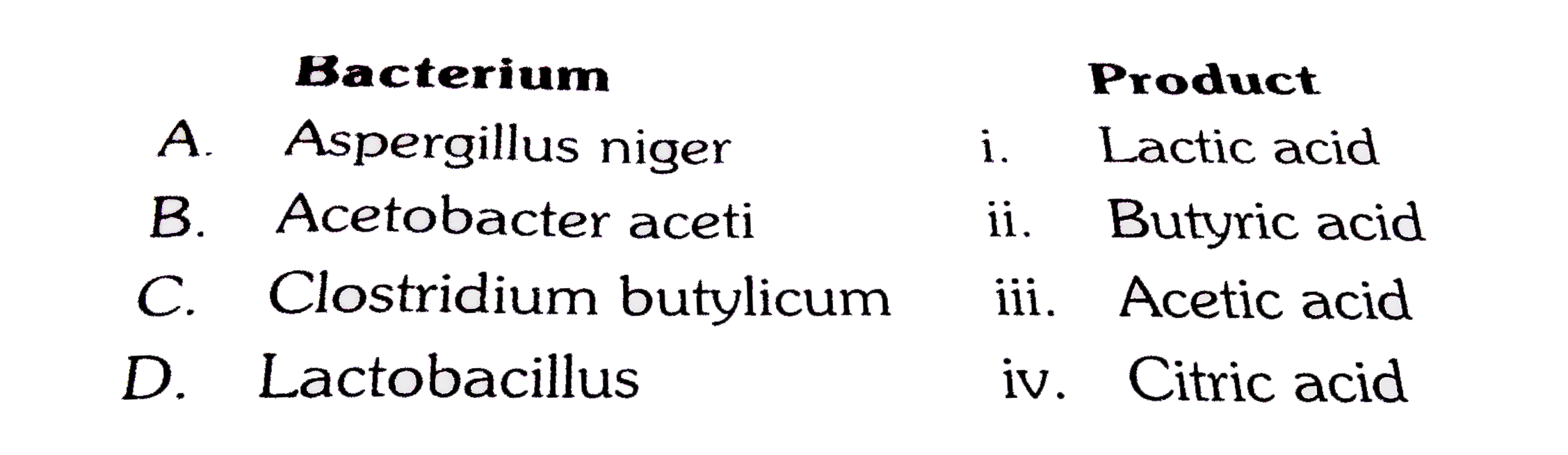
View SolutionMatch the following list of bacteria and their commerically important products :

View Solution


