On a certain sum of money, the difference between the compound interest for a year,payable half-yearly, and the simple interest for a year is रु 180/-. Find the sum lent out, if the rate of interest in both the cases is 10% per annum.
The correct Answer is:रु 72.000
To solve the problem step by step, we will follow the process of calculating the simple interest and compound interest, and then use the information given to find the sum lent out.
Step 1: Define the variables
Let the sum of money (principal) be P.
Step 2: Calculate Simple Interest (SI)
The formula for Simple Interest is:
SI=P×R×T100
Where:
- R is the rate of interest (10% per annum)
- T is the time (1 year)
Substituting the values:
SI=P×10×1100=P×10100=P10
Step 3: Calculate Compound Interest (CI) for half-yearly compounding
Since the interest is compounded half-yearly, the rate for each half year is:
Half-yearly rate=102=5%
For the first half year:
CI1=P×5×0.5100=P×5200=P40
After the first half year, the amount becomes:
A1=P+CI1=P+P40=P(1+140)=P(4140)
For the second half year, we calculate the interest on the new amount:
CI2=A1×5100=P(4140)×5100=41P×54000=205P4000=P20
Step 4: Total Compound Interest for the year
CI=CI1+CI2=P40+P20
To add these fractions, we need a common denominator:
CI=P40+2P40=3P40
Step 5: Find the difference between Compound Interest and Simple Interest
According to the problem, the difference between CI and SI is given as:
CI−SI=180
Substituting the values we calculated:
3P40−P10=180
Step 6: Simplify the equation
To simplify, convert P10 to a fraction with a denominator of 40:
P10=4P40
Now, substituting back:
3P40−4P40=180
−P40=180
Step 7: Solve for P
Multiplying both sides by -40:
P=−180×40=−7200
Since we are dealing with money, we take the absolute value:
P=7200
Final Answer
The sum lent out is ₹ 7200.
---
Let the sum of money (principal) be P.
The formula for Simple Interest is:
SI=P×R×T100
Where:
- R is the rate of interest (10% per annum)
- T is the time (1 year)
SI=P×10×1100=P×10100=P10
Since the interest is compounded half-yearly, the rate for each half year is:
Half-yearly rate=102=5%
CI1=P×5×0.5100=P×5200=P40
A1=P+CI1=P+P40=P(1+140)=P(4140)
CI2=A1×5100=P(4140)×5100=41P×54000=205P4000=P20
CI=CI1+CI2=P40+P20
To add these fractions, we need a common denominator:
CI=P40+2P40=3P40
According to the problem, the difference between CI and SI is given as:
CI−SI=180
Substituting the values we calculated:
3P40−P10=180
To simplify, convert P10 to a fraction with a denominator of 40:
P10=4P40
Now, substituting back:
3P40−4P40=180
−P40=180
Multiplying both sides by -40:
P=−180×40=−7200
Since we are dealing with money, we take the absolute value:
P=7200
The sum lent out is ₹ 7200.
Topper's Solved these Questions
- COMPOUND INTEREST BOOK - ICSECHAPTER - COMPOUND INTEREST EXERCISE - EXERCISE 2 (C)
12 Videos
- COMPOUND INTEREST BOOK - ICSECHAPTER - COMPOUND INTEREST EXERCISE - EXERCISE 2 (D)
10 Videos
- COMPOUND INTEREST BOOK - ICSECHAPTER - COMPOUND INTEREST EXERCISE - EXERCISE 2 (A)
10 Videos
- COMPLEMENTARY ANGLESBOOK - ICSECHAPTER - COMPLEMENTARY ANGLESEXERCISE - EXERCISE
64 Videos
- COMPOUND INTEREST (USING FORMULA)BOOK - ICSECHAPTER - COMPOUND INTEREST (USING FORMULA)EXERCISE - EXERCISE 3(E)
24 Videos
Similar Questions
A sum is invested at compound interest compounded yearly. If the interest for two successive years be रु 5,700 and रु 7,410, calculate the rate of interest .
View SolutionWhat sum will amount to रु 6,593.40 in 2 years at C.I., if the rates are 10 percent and 11 percent for the two successive years ?
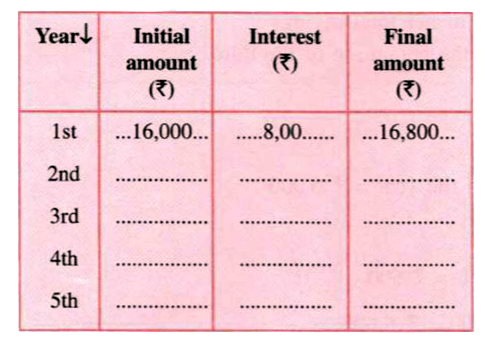
View Solution16,000 is invested at 5% compound interest compounded per annum. Use the table, given below, to find the amount in 4 years.
View SolutionEvaluate:
cos22∘sin68∘
View SolutionSimple interest on a sum of money for 2 years at 4% growth rate is Rs 450. Find compound interest on the same sum and at the same rate for 1 year, if the interest is reckoned half yearly.
View SolutionThe difference between compound interest and simple interest on a sum of money lent for 2 years at the rateof 10% is Rs40. The sum is :
View SolutionA sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then interest is Rs 482 more. Find the sum.
View Solutionयदि ब्याज वार्षिक सयोजिता हो तो किसी धनराशि पर 10 % वार्षिक दर से 2 वर्ष का चक्रवृद्धि तथा साधरण ब्याज का अंतर रूपए 28 है| यदि वार्षिक ब्याज दर छमाही हो तो दोनों तरह के ब्याजों मे किंतना अंतर है |
View SolutionThe difference between compound interest at 10% per annum and simple interest at 8% per annum on a certain sum for 3 years is Rs 910. Find the sum.
View SolutionA person lent out certain sum on simple interest and the same sum on compound interest at a certain rate of interest per annum. He noticed that the ratio between the difference of compound interest and simple interest of 3 years and 2 years is 16:49. The rate of interest per annum is
View SolutionA sum of money was lent for 2 years at 20% compounded annually. If the interest is payable half-yearly instead of yearly, then interest is Rs 482 more. Find the sum.
View SolutionIf the difference of the compound interest and the simple interest on a sum of money for 3 years is Rs. 78. Find the sum of money, if the rate of interest in both case be 10%
View SolutionThe difference between compound interest for a year payable half-yearly and simple interest on a certain sum of money lent out at 10% for a year is Rs 15. Find the sum of money lent out.
View SolutionThe compound interest, calculated yearly, on a certain sum of money for the second year is रु 1,089 and for the third year it is? रु 1,197.90. Calculate the rate of interest and the sum of money.
View SolutionFind the sum of money if the difference between compound interest and simple interest for 3 years becomes Rs 930 at the rate of 10% interest per annum.
View Solution
