P is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
In△ABP
AB=AP
∠APB=∠ABP(Angles opposing to equal sizes are equal)
∠BPA=∠APC=180∘(Linear pair)
∠APC=180∘−∠BPA ........(1)
∠PAD+∠APC=180∘(co interrior angles)
∠PAD=180∘−∠APC=180∘−180∘+∠BPA
In△ABP
AB=AP
∠APB=∠ABP(Angles opposing to equal sizes are equal)
∠BPA=∠APC=180∘(Linear pair)
∠APC=180∘−∠BPA ........(1)
∠PAD+∠APC=180∘(co interrior angles)
∠PAD=180∘−∠APC=180∘−180∘+∠BPA
∠PAD=∠BPA.......(ii)
∠PAD+∠ACD=180∘(co interior ∠s)
∠ADC=180∘−∠PAD=180∘−∠BPA.......(from (ii))
∠ADC+∠BPA=180∘
In△ABP
AB=AP
∠APB=∠ABP(Angles opposing to equal sizes are equal)
∠BPA=∠APC=180∘(Linear pair)
∠APC=180∘−∠BPA ........(1)
∠PAD+∠APC=180∘(co interrior angles)
∠PAD=180∘−∠APC=180∘−180∘+∠BPA
In△ABP
AB=AP
∠APB=∠ABP(Angles opposing to equal sizes are equal)
∠BPA=∠APC=180∘(Linear pair)
∠APC=180∘−∠BPA ........(1)
∠PAD+∠APC=180∘(co interrior angles)
∠PAD=180∘−∠APC=180∘−180∘+∠BPA
∠PAD=∠BPA.......(ii)
∠PAD+∠ACD=180∘(co interior ∠s)
∠ADC=180∘−∠PAD=180∘−∠BPA.......(from (ii))
∠ADC+∠BPA=180∘
∠ADC+∠ABP=180∘( ∠BPA=∠ABP)
Since sum of opposite angles of the quadilateral is 180∘
Hence the quadilateral ABCD is a cyclic quadilateral.
Topper's Solved these Questions
Similar Questions
P is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
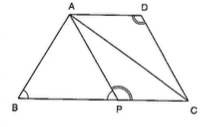
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of PQR is double the perimeter of ABC
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming PQR.Figure .Show that BC=12QR
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
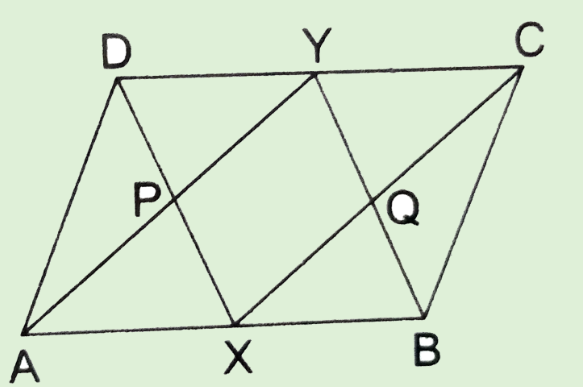
View Solution