P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
Step by step video & text solution for P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(triangleAPD) = ar(triangleCPD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023टॉपर्स ने हल किए ये सवाल
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:NCERT SECTION ( EXERCISE 9.1)
Explore 1 Video
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:NCERT SECTION ( EXERCISE 9.2)
Explore 7 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:Olympiad/HOTS Corner
Explore 14 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
समान प्रश्न
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
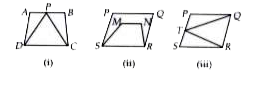

View SolutionIn the given figure ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm,find AD.

View SolutionIn the given figure ABCD is a rectangle and all measurements are in centimeters. Find the area of the shaded region.
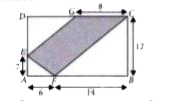
View SolutionABCD is a cyclic quadrilateral, if ∠BAC=60∘,∠BCA=20∘, then find the value of ∠ADC.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View Solutionचतुर्भुज ACBD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD)=ar(BOC) है सिद्ध कीजिए कि ABCD एक समलंब है
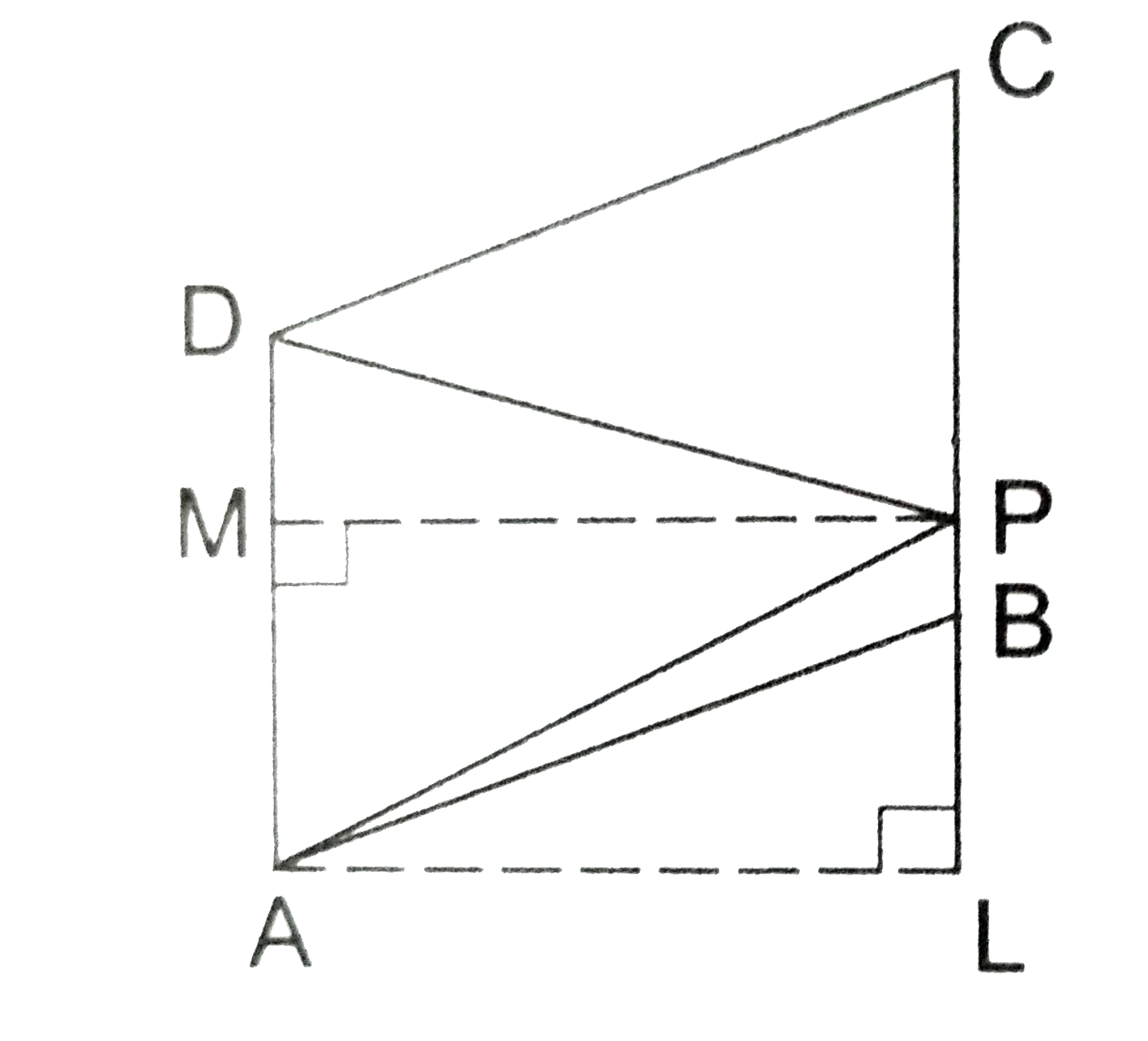
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View Solutionएक समांतर चतुर्भुज ABCD के विकर्ण BD पर कोई बिंदु O स्थित है, तो सिद्ध कीजिए कि ar(ΔOAB)=ar(ΔOBC)
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण O पर प्रतिच्छेद करते है। यदि BO पर कोई बिंदु P हो तो सिद्ध कीजिए कि :
(i)ar(ΔADO)=ar(ΔCDO) (ii)ar(ΔABP)=ar(ΔCBP)
View Solutionएक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ΔAPD=ΔCPD.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC) . Prove that ABCD is a trapezium.
View SolutionABCD is a parallelogram. The diagonals AC and BD intersect each other at ‘O’. Prove that ar(ΔAOD)=ar(ΔBOC) . (Hint: Congruent figures have equal area)
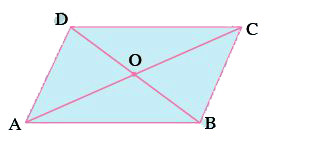
View Solution