PQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is △ . Then prove that the height of the tower is (abc) tanθ4'△'.Solution in Bengali
Let the height of the tower PQ be h.
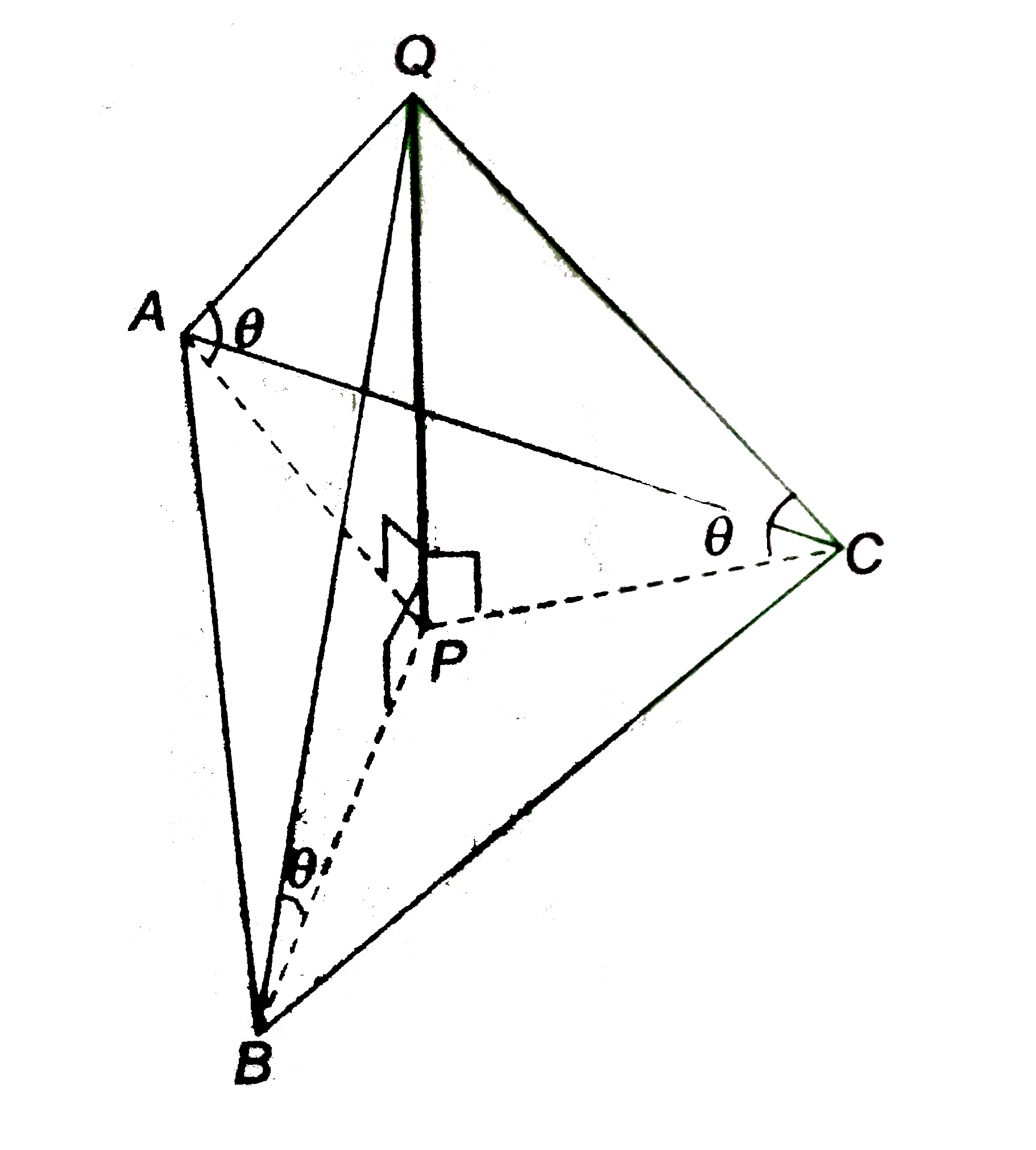
AP = BP =CP =hcotθ
Therefore , P is the circumcentre of ΔABC
∴AP=BP=CP=R=abc4Δ
∴h=abc4Δtanθ
Similar Questions
A vertical tower CP subtends the same angle θ, at point B on the horizontal plane through C, the foot of the tower, and at point A in the vertical plane. If the triangle ABC is equilateral with length of each side equal to 4 m, the height of the tower is
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is △ . Then prove that the height of the tower is (abc) tanθ4'△'.
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View Solutionएक मीनार के सिरे का भुमि पर त्रिभुज बनाने वाले तीन बिन्दुओं A,B,C में से प्रत्येक से उन्यन कोण समान तथा α के बराबर है यदि त्रिभुज ABC के परित्रिज्या R हैं तब मीनार की ऊँचाई है
View SolutionThe angle of elevation of the top of the tower observed from each of three points A,B , C on the ground, forming a triangle is the same angle α. If R is the circum-radius of the triangle ABC, then find the height of the tower
View SolutionThe angle of elevation of the top of the tower observed from each of the three points A,B,C on the ground, forming a triangle is the same angle ∝. If R is the circum-radius of the triangle ABC, then the height of the tower is
View SolutionA tower stands vertically on the ground. From a point which is 15 meter away from the foot of the tower, the angle of elevation of the top of the tower is 45∘. What is the height of the tower?
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is △ . Then prove that the height of the tower is (abc) tanθ4'△'.
View Solution

