Prove that any line segment drawn from the vertex of a triangle to the base is bisected by the line segment joining the midpoints of the other sides of the triangle.
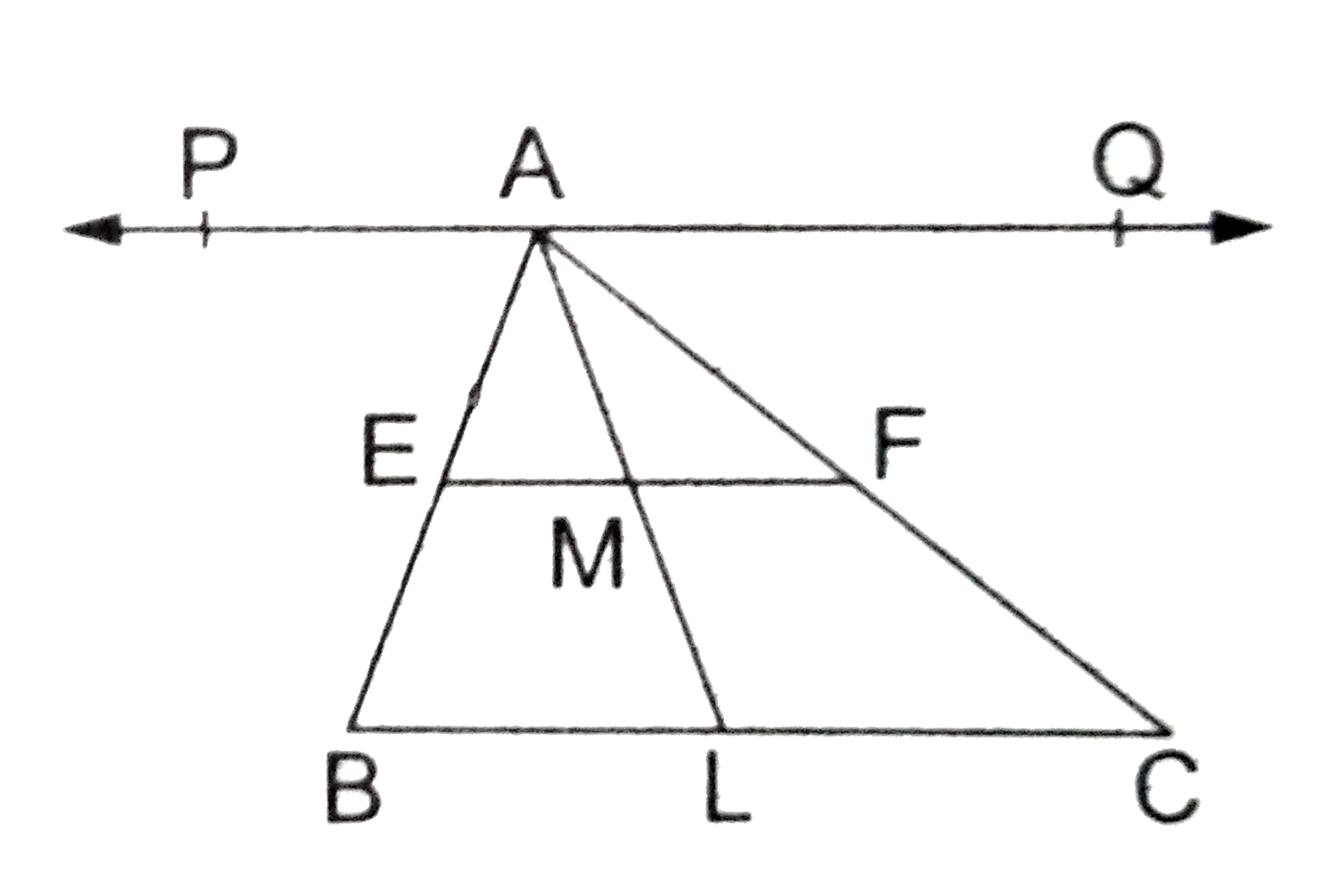
Let △ABC be a given triangle in which E and F are F are the midpoints of AB and AC respectively. Let AL be a line segment drawn from vertex A to the base BC, meeting BC at L and EF at M.
We have to show AM = ML.
Through A, draw PAQ||BC.
In △ABC, E and F being the midpoints of AB and AC respectively, we have EF||BC.
Now, PAQ, EF and BC are three parallel lines such that the intercepts AE and EB made by them on transversal AEB are equal.
∴ the intercepts AM and ML made by them on transversal AML must be equal.
Hence, AM = ML.
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionThe equation of straight line shown in figure is :
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_020_Q01.png" width="80%"gt
View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View SolutionFind out area of triangle OAB and BCD shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View Solution'A' is the portion of adenophypophysis which secrets different hormones 'A' is____
View Solution
