Prove that for every positive number s satisfying the condition s2>2 one can always find a smaller rational number s−k(k>0), forwhich (s−k)2>2.
The correct Answer is:You may take k=s2−22s
Topper's Solved these Questions
- INTRODUCTION OF MATHEMATICAL ANALYSISBOOK - IA MARONCHAPTER - INTRODUCTION OF MATHEMATICAL ANALYSISEXERCISE - Function. Domain of Definition
21 Videos
- INTRODUCTION OF MATHEMATICAL ANALYSISBOOK - IA MARONCHAPTER - INTRODUCTION OF MATHEMATICAL ANALYSISEXERCISE - Investigation of Functions
15 Videos
- INDEFINITE INTEGRALS, BASIC METHODS OF INTEGRATIONBOOK - IA MARONCHAPTER - INDEFINITE INTEGRALS, BASIC METHODS OF INTEGRATIONEXERCISE - 4.4. Reduction Formulas
2 Videos
- THE DEFINITE INTEGRAL BOOK - IA MARONCHAPTER - THE DEFINITE INTEGRAL EXERCISE - 6 . 8 (Additional Problems)
3 Videos
Similar Questions
Given the function f(x)=(x+1)(x−1)
Find f(2x),2f(x),f(x2),[f(x)]2.
View Solution(a) Find the minimum value of the function y=3x2+5x−1
(b) Find the reactangle with the maximum area from among all rectangles of a given perimeter.
View SolutionIntegrating by parts, derive reduction formulas for calculating the following integrals :
(a) In=∫dx(x2+a2)n,
View SolutionGiven the function f(x)=⎧⎪⎨⎪⎩1−x at 0≤x≤10 at 1<x≤2(2−x)2at 2<x≤3
Check directly that the function
F(x)=∫x0f(t)dt
is continuous on the interval [0,3] and that its derivative at each interior point of this interval exists and is equal to f(x)
View SolutionLet S(k) = 1 + 3 + 5 +...+ (2k -1) = 3 + k^2 . Then which of the following is true ? (A) S(1) is correct (B) S(k)=S(k+1) (C) S(k) != S(k+1) (D) Principal of mathematical induction can be used to prove the formula
View SolutionEvaluate limx→0k[x]−1−|x|InKx2,k>0
View SolutionLet a and b be positive real numbers with a3+b3=a−bandk=a2+4b2 , then (1)k<1 (2) k>1 (3) k=1(4) k>2
View Solution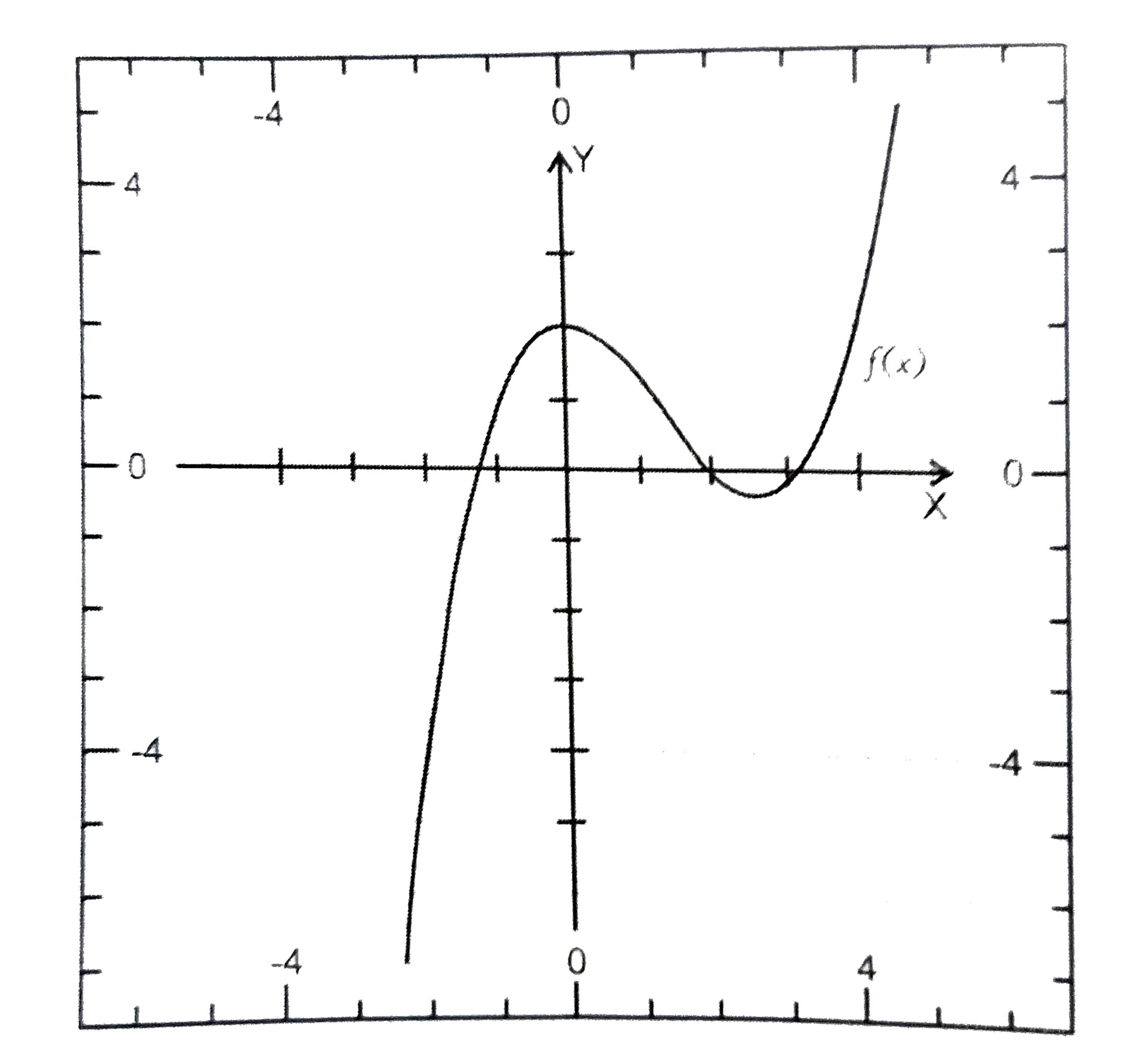
What is the number of possible values of K (5>k>0) such that g(x) = f(x) -k has exactly one root ?
View SolutionIf s be the sum of n positive unequal quantities a, b, c then prove the inequality ,
ss−a+ss−b+ss−c+……>n2n−1(n≥2).
View SolutionThe equation x21−k−y21+k=1,k>1 represents s
View SolutionFind the value of 2551 S where S=50∑k=1kk4+k2+1
View SolutionIf kx2−4x+3k+1>0 for atleast one x>0, then if k∈S contains :
View Solution{:("COLUMN-I","COLUMN-II"),((A)"Thermal stability",(p)H_(2)Te gt H_(2)Se gt H_(2)S gt H_(2)O),((B)"Acidic nature",(q)H_(2)O gt H_(2)S gt H_(2)Se gt H_(2)Te),((C )"Boiling points",(r )H_(2)S lt H_(2)Se lt H_(2)Te lt H_(2)O),((D) angleM MH " Bond angle",(s) H_(2)S gt H_(2)Se gt H_(2)Te=H_(2)Po):}
View SolutionLet P(n):sn>n∀n∈N and 2k>k,∀n=K then which of the following is true ∀k≥2?
View SolutionIf kx2−4x+3k+1>0 for atleast one x>0, then if k∈S contains :
View Solution

