Prove that opposites of a quadrilaterial circumscribing a circle subtend supplementary angles at the centre of the circle. Solution in Kannada
The correct Answer is:180∘
Step by step video, text & image solution for Prove that opposites of a quadrilaterial circumscribing a circle subtend supplementary angles at the centre of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionA circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
View SolutionProve tht the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
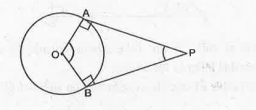
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the opposite sides of a quadrilateral circumscribing a
circle subtend supplementary angles at the centres of the circle.
View Solution
