Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
Step by step video solution for Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:OSWAL PUBLICATIONChapter:TRIANGLESExercise:BOARD CORNER ( VERY SHORT ANSWER TYPE QUESTION ( 1 MARK EACH ))
Explore 4 Videos
- TRIANGLESBook:OSWAL PUBLICATIONChapter:TRIANGLESExercise:BOARD CORNER ( SHORT ANSWER TYPE QUESTION ( 3 MARK EACH ))
Explore 6 Videos
- TRIANGLESBook:OSWAL PUBLICATIONChapter:TRIANGLESExercise:NCERT EXEMPLAR ( EXERCISE - 6.3 )
Explore 15 Videos
- SURFACE AREAS AND VOLUMES Book:OSWAL PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
Explore 9 Videos
Similar Questions
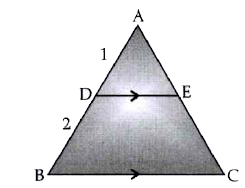
In Figure 1 DE|| BC ,AD = 1 cm and BD =2 cm . What is the ratio of the ar (ΔABC) to the ar(ΔADE) ?
View SolutionIn the given figure, ∠ACB=90∘andCD⊥AB. Prove that CD2=BD⋅AD

View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionA bucket is in form of a frustum of a cone with a copacity of 12308.8cm3of water. The radii of the tope bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. [ Use π=3.14.]
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionIn a right -angle triangle, the length of the sides containing the right angles area aandb. With the mid-point of each sides as centres three semicircles are drawn outiside the triangle. Find the area of Δ and the semicircles together
View SolutionIn a right-angled triangle, the area of a square drawn on the hypotenuse is equal to the …............... of the areas of the squares drawn on other two sides.
View SolutionProve that if equilateral triangles are drawn on the sides of a right-angled triangles then the area of the equilateral triangle, drawn on the hypotenuse is equal to the sum of the areas of the other two equilateral triangals drawn on its other two sides.
View SolutionEquilateral triangle are drawn on the three sides of a right angled Triangle. Show that the area of the Triangle on the hypotenuse is equal to the sum of the areas of triangle on the other two sides.
View SolutionEquilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionEquilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionEquilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View Solutionশূন্যস্থান পূরণ করো: একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের __ সমান ।
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View Solution